机器学习——Logistic Regression

阅读数: 次 2022-09-29

本文基于Sakura-gh大佬的机器学习笔记修改，仅作为学习资料备用，如有侵权，联系作者。

Logistic Regression

Review

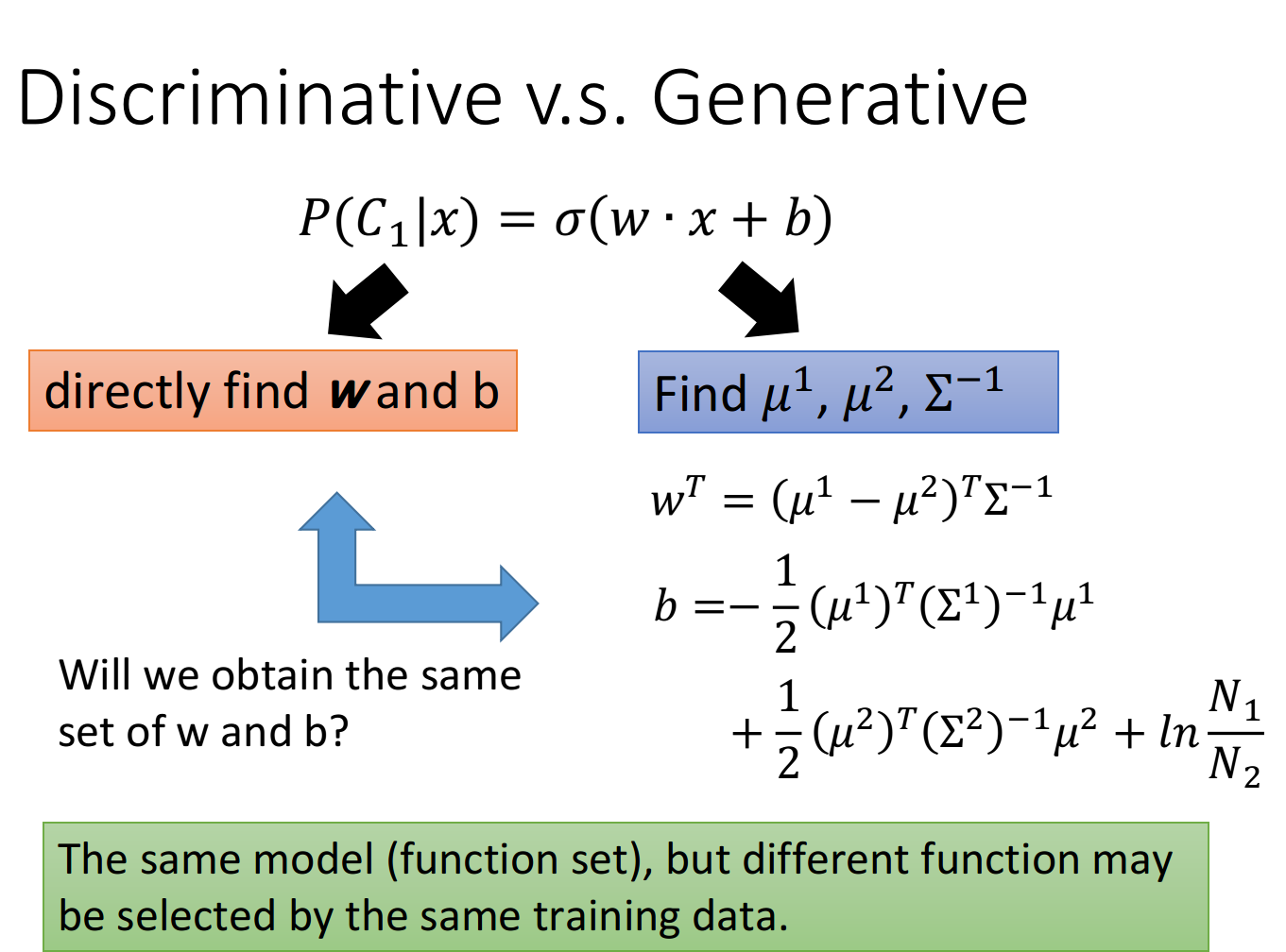
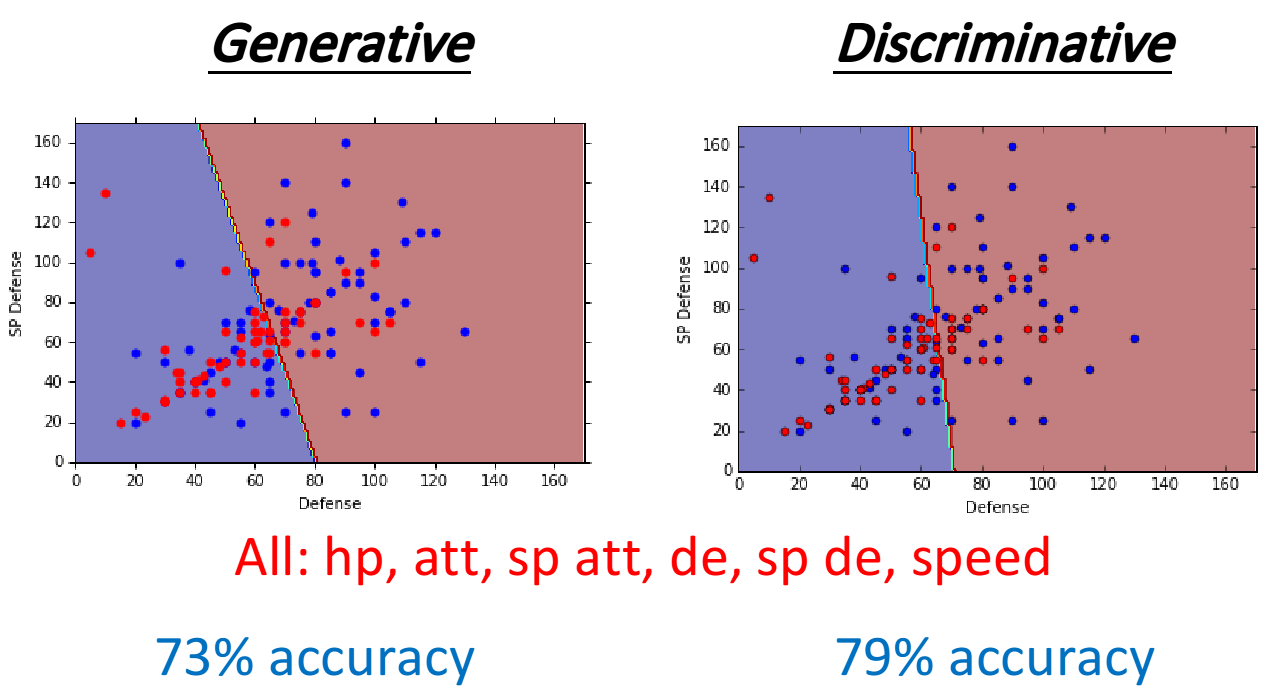
在classification这一章节，我们讨论了如何通过样本点的均值$u$和协方差$\Sigma$来计算$P(C_1),P(C_2),P(x|C_1),P(x|C_2)$，进而利用$P(C_1|x)=\frac{P(C_1)P(x|C_1)}{P(C_1)P(x|C_1)+P(C_2)P(x|C_2)}$计算得到新的样本点x属于class 1的概率，由于是二元分类，属于class 2的概率$P(C_2|x)=1-P(C_1|x)$

之后我们还推导了$P(C_1|x)=\sigma(z)=\frac{1}{1+e^{-z}}$，并且在Gaussian的distribution下考虑class 1和class 2共用$\Sigma$，可以得到一个线性的z(其实很多其他的Probability model经过化简以后也都可以得到同样的结果)

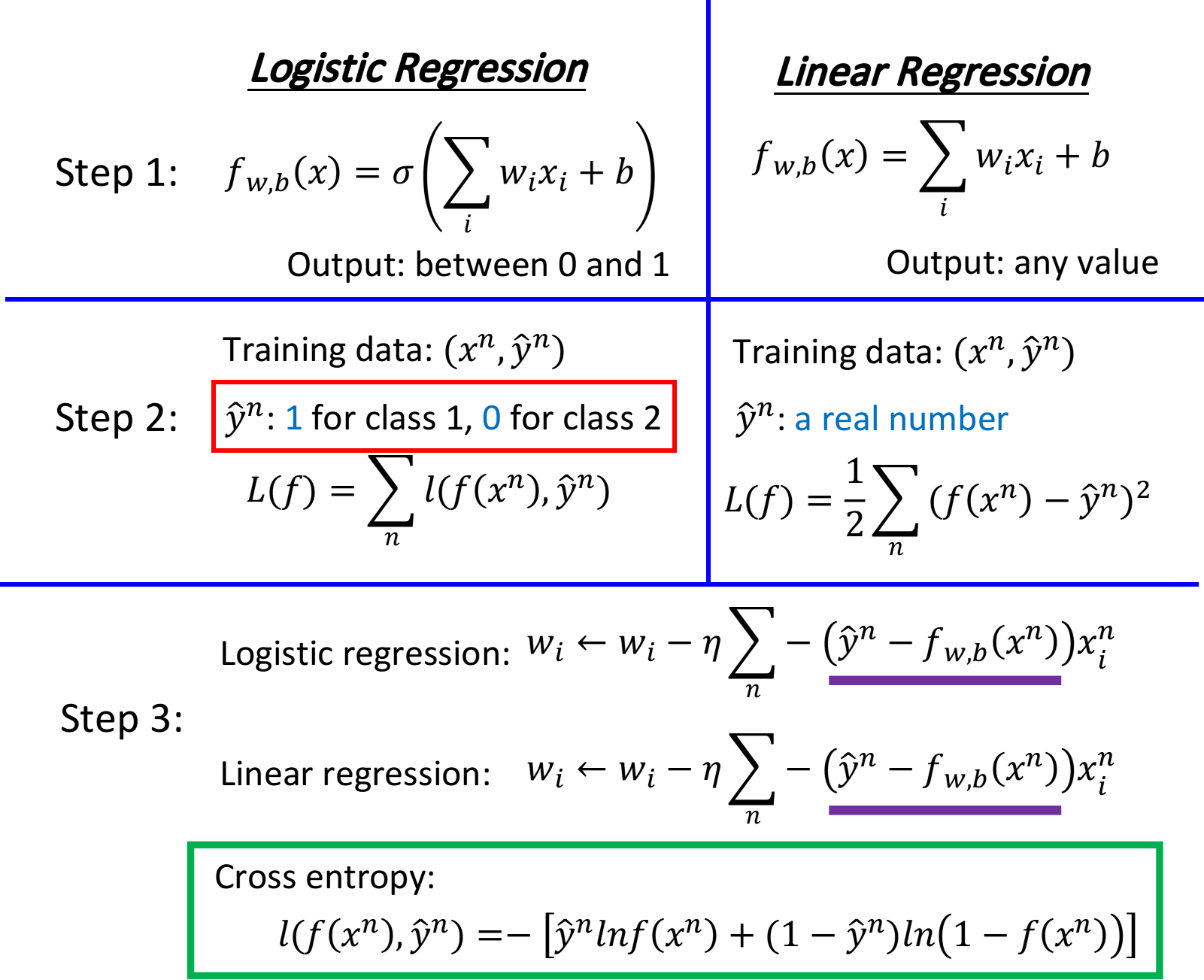
$P_{w,b}(C_1|x)=\sigma(z)=\frac{1}{1+e^{-z}} \\ z=w\cdot x+b=\sum\limits_i w_ix_i+b \\$

这里的w和x都是vector，两者的乘积是inner product，从上式中我们可以看出，现在这个model(function set)是受w和b控制的，因此我们不必要再去像前面一样计算一大堆东西，而是用这个全新的由w和b决定的model——Logistic Regression(逻辑回归)

Three Steps of machine learning

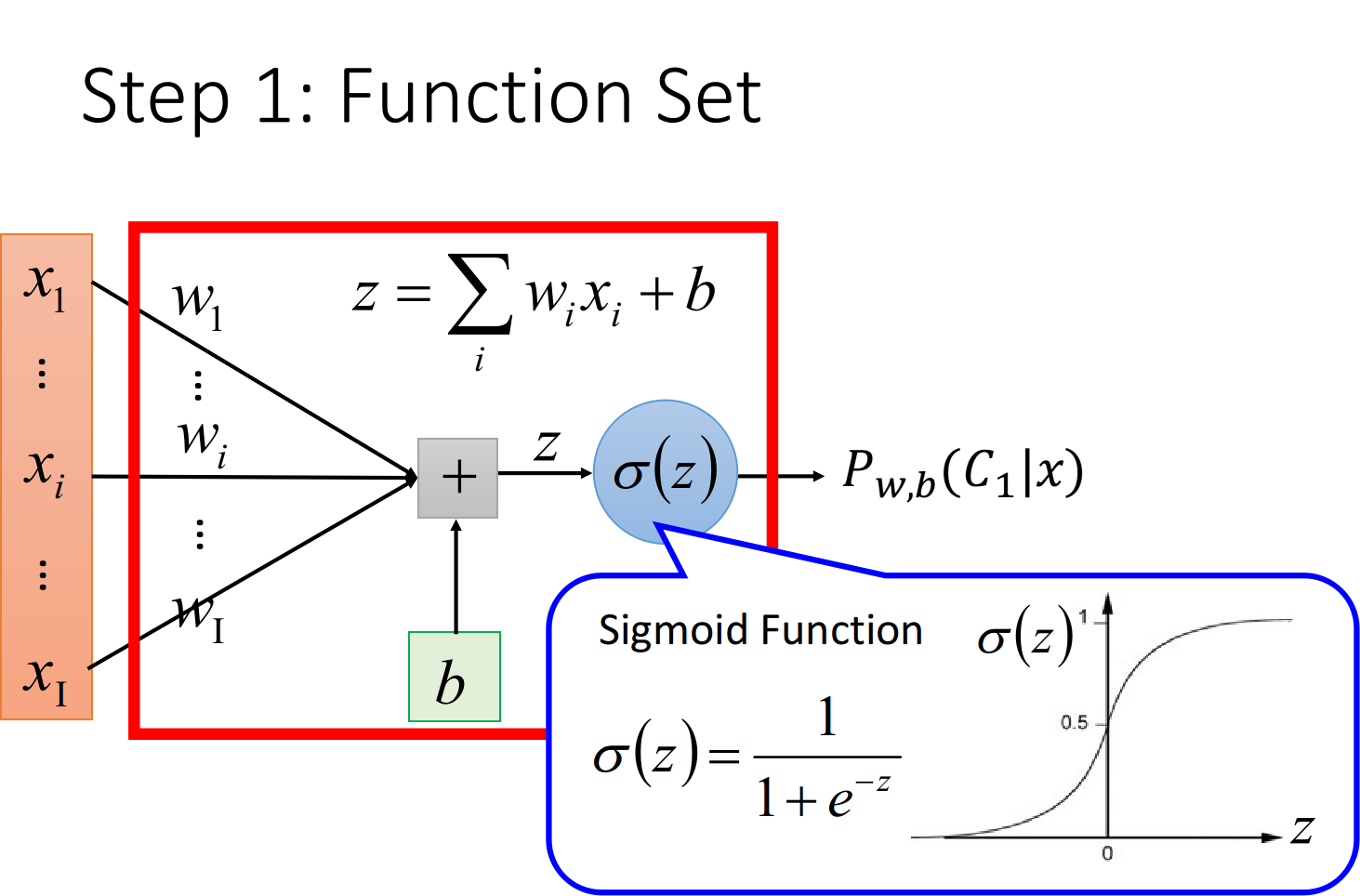
Step 1：function set

这里的function set就是Logistic Regression——逻辑回归

$w_i$：weight，$b$：bias，$\sigma(z)$：sigmoid function，$x_i$：input

##### Step 2：Goodness of a function 现在我们有N笔Training data，每一笔data都要标注它是属于哪一个class 假设这些Training data是从我们定义的posterior Probability中产生的(后置概率，某种意义上就是概率密度函数)，而w和b就决定了这个posterior Probability，那我们就可以去计算某一组w和b去产生这N笔Training data的概率，利用极大似然估计的思想，最好的那组参数就是有最大可能性产生当前N笔Training data分布的$w^*$和$b^*$ 似然函数只需要将每一个点产生的概率相乘即可，注意，这里假定是二元分类，class 2的概率为1减去class 1的概率

由于$L(w,b)$是乘积项的形式，为了方便计算，我们将上式做个变换： $$ \begin{split} &w^*,b^*=\arg \max\limits_{w,b} L(w,b)=\arg\min\limits_{w,b}(-\ln L(w,b)) \\ &\begin{equation} \begin{split} -\ln L(w,b)=&-\ln f_{w,b}(x^1)\\ &-\ln f_{w,b}(x^2)\\ &-\ln(1-f_{w,b}(x^3))\\ &\ -... \end{split} \end{equation} \end{split} $$ 由于class 1和class 2的概率表达式不统一，上面的式子无法写成统一的形式，为了统一格式，这里将Logistic Regression里的所有Training data都打上0和1的标签，即output $\hat{y}=1$代表class 1，output $\hat{y}=0$代表class 2，于是上式进一步改写成： $$ \begin{split} -\ln L(w,b)=&-[\hat{y}^1 \ln f_{w,b}(x^1)+(1-\hat{y}^1)ln(1-f_{w,b}(x^1))]\\ &-[\hat{y}^2 \ln f_{w,b}(x^2)+(1-\hat{y}^2)ln(1-f_{w,b}(x^2))]\\ &-[\hat{y}^3 \ln f_{w,b}(x^3)+(1-\hat{y}^3)ln(1-f_{w,b}(x^3))]\\ &\ -... \end{split} $$ 现在已经有了统一的格式，我们就可以把要minimize的对象写成一个summation的形式： $$ -\ln L(w,b)=\sum\limits_n -[\hat{y}^n \ln f_{w,b}(x^n)+(1-\hat{y}^n) \ln(1-f_{w,b}(x^n))] $$ 这里$x^n$表示第n个样本点，$\hat{y}^n$表示第n个样本点的class标签(1表示class 1,0表示class 2)，最终这个summation的形式，里面其实是两个Bernouli distribution(两点分布)的cross entropy(交叉熵)

假设有如上图所示的两个distribution p和q，它们的交叉熵就是$H(p,q)=-\sum\limits_{x} p(x) \ln (q(x))$，这也就是之前的推导中在$-\ln L(w,b)$前加一个负号的原因 cross entropy交叉熵的含义是表达这两个distribution有多接近，如果p和q这两个distribution一模一样的话，那它们算出来的cross entropy就是0(详细解释在“信息论”中)，而这里$f(x^n)$表示function的output，$\hat{y}^n$表示预期的target，因此**交叉熵实际上表达的是希望这个function的output和它的target越接近越好** 总之，我们要找的参数实际上就是： $$ w^*,b^*=\arg \max\limits_{w,b} L(w,b)=\arg\min\limits_{w,b}(-\ln L(w,b)=\sum\limits_n -[\hat{y}^n \ln f_{w,b}(x^n)+(1-\hat{y}^n) \ln(1-f_{w,b}(x^n))] $$ ##### step 3：Find the best function 实际上就是去找到使loss function即交叉熵之和最小的那组参数$w^*,b^*$就行了，这里用gradient descent的方法进行运算就ok 这里sigmoid function的微分可以直接作为公式记下来：$\frac{\partial \sigma(z)}{\partial z}=\sigma(z)(1-\sigma(z))$，sigmoid和它的微分的图像如下：

先计算$-\ln L(w,b)=\sum\limits_n -[\hat{y}^n \ln f_{w,b}(x^n)+(1-\hat{y}^n) \ln(1-f_{w,b}(x^n))]$对$w_i$的偏微分，这里$\hat{y}^n$和$1-\hat{y}^n$是常数先不用管它，只需要分别求出$\ln f_{w,b}(x^n)$和$\ln (1-f_{w,b}(x^n))$对$w_i$的偏微分即可，整体推导过程如下：

将得到的式子进行进一步化简，可得：

我们发现最终的结果竟然异常的简洁，gradient descent每次update只需要做： $$ w_i=w_i-\eta \sum\limits_{n}-(\hat{y}^n-f_{w,b}(x^n))x_i^n $$ 那这个式子到底代表着什么意思呢？现在你的update取决于三件事： * learning rate，是你自己设定的 * $x_i$，来自于data * $\hat{y}^n-f_{w,b}(x^n)$，代表function的output跟理想target的差距有多大，如果离目标越远，update的步伐就要越大 #### Logistic Regression V.s. Linear Regression 我们可以把逻辑回归和之前将的线性回归做一个比较 ##### compare in step1 Logistic Regression是把每一个feature $x_i$加权求和，加上bias，再通过sigmoid function，当做function的output 因为Logistic Regression的output是通过sigmoid function产生的，因此一定是介于0~1之间；而linear Regression的output并没有通过sigmoid function，所以它可以是任何值 ##### compare in step2 在Logistic Regression中，我们定义的loss function，即要去minimize的对象，是所有example(样本点)的output( $f(x^n)$ )和实际target( $\hat{y}^n$ )在Bernoulli distribution(两点分布)下的cross entropy(交叉熵)总和 **交叉熵**的描述：这里把$f(x^n)$和$\hat{y}^n$各自看做是一个**Bernoulli distribution(两点分布)**，那它们的cross entropy $l(f(x^n),\hat{y}^n)=-[\hat{y}^n \ln f(x^n)+(1-\hat{y}^n) \ln (1-f(x^n))]$之和，就是我们要去minimize的对象，直观来讲，就是**希望function的output $f(x^n)$和它的target $\hat{y}^n$越接近越好** 注：这里的“看做”只是为了方便理解和计算，并不是真的做出它们是两点分布的假设而在linear Regression中，loss function的定义相对比较简单，就是单纯的function的output( $f(x^n)$ )和实际target( $\hat{y}^n$ )在数值上的平方和的均值这里可能会有一个疑惑，为什么Logistic Regression的loss function不能像linear Regression一样用square error来表示呢？后面会有进一步的解释 ##### compare in step3 神奇的是，Logistic Regression和linear Regression的$w_i$update的方式是一模一样的，唯一不一样的是，Logistic Regression的target $\hat{y}^n$和output $f(x^n)$都必须是在0和1之间的，而linear Regression的target和output的范围可以是任意值

#### Logistic Regression + Square error？之前提到了，为什么Logistic Regression的loss function不能用square error来描述呢？我们现在来试一下这件事情，重新做一下machine learning的三个step

现在会遇到一个问题：如果第n个点的目标target是class 1，则$\hat{y}^n=1$，此时如果function的output $f_{w,b}(x^n)=1$的话，说明现在离target很接近了，$f_{w,b}(x)-\hat{y}$这一项是0，于是得到的微分$\frac{\partial L}{\partial w_i}$会变成0，这件事情是很合理的；但是当function的output $f_{w,b}(x^n)=0$的时候，说明离target还很遥远，但是由于在step3中求出来的update表达式中有一个$f_{w,b}(x^n)$，因此这个时候也会导致得到的微分$\frac{\partial L}{\partial w_i}$变成0 如果举class 2的例子，得到的结果与class 1是一样的如果我们把参数的变化对total loss作图的话，loss function选择cross entropy或square error，参数的变化跟loss的变化情况可视化出来如下所示：(黑色的是cross entropy，红色的是square error)

假设中心点就是距离目标很近的地方，如果是cross entropy的话，距离目标越远，微分值就越大，参数update的时候变化量就越大，迈出去的步伐也就越大但当你选择square error的时候，过程就会很卡，因为距离目标远的时候，微分也是非常小的，移动的速度是非常慢的，我们之前提到过，实际操作的时候，当gradient接近于0的时候，其实就很有可能会停下来，因此使用square error很有可能在一开始的时候就卡住不动了，而且这里也不能随意地增大learning rate，因为在做gradient descent的时候，你的gradient接近于0，有可能离target很近也有可能很远，因此不知道learning rate应该设大还是设小综上，尽管square error可以使用，但是会出现update十分缓慢的现象，而使用cross entropy可以让你的Training更顺利 #### Discriminative v.s. Generative ##### same model but different currency Logistic Regression的方法，我们把它称之为discriminative的方法；而我们用Gaussian来描述posterior Probability这件事，我们称之为Generative的方法

实际上它们用的model(function set)是一模一样的，都是$P(C_1|x)=\sigma(w\cdot x+b)$，如果是用Logistic Regression的话，可以用gradient descent的方法直接去把b和w找出来；如果是用Generative model的话，我们要先去算$u_1,u_2,\Sigma^{-1}$，然后算出b和w 你会发现用这两种方法得到的b和w是不同的，尽管我们的function set是同一个，但是由于做了不同的假设，最终从同样的Training data里找出来的参数会是不一样的在Logistic Regression里面，我们**没有做任何实质性的假设**，没有对Probability distribution有任何的描述，我们就是单纯地去找b和w(推导过程中的假设只是便于理解和计算，对实际结果没有影响) 而在Generative model里面，我们对Probability distribution是**有实质性的假设**的，之前我们假设的是Gaussian(高斯分布)，甚至假设在相互独立的前提下是否可以是naive bayes(朴素贝叶斯)，根据这些假设我们才找到最终的b和w 哪一个假设的结果是比较好的呢？Generative model和discriminative model的预测结果比较如下：

实际上Discriminative的方法常常会比Generative的方法表现得更好，这里举一个简单的例子来解释一下 ##### toy example 假设总共有两个class，有这样的Training data：每一笔data有两个feature，总共有1+4+4+4=13笔data 如果我们的testing data的两个feature都是1，凭直觉来说会认为它肯定是class 1，但是如果用naive bayes的方法(朴素贝叶斯假设所有的feature相互独立，方便计算)，得到的结果又是怎样的呢？

通过Naive bayes得到的结果竟然是这个测试点属于class 2的可能性更大，这跟我们的直觉比起来是相反的，实际上我们直觉认为两个feature都是1的测试点属于class 1的可能性更大是因为我们潜意识里认为这两个feature之间是存在某种联系的，但是对Naive bayes来说，它是不考虑不同dimension之间的correlation，Naive bayes认为在dimension相互独立的前提下，class 2没有sample出都是1的data，是因为sample的数量不够多，如果sample够多，它认为class 2观察到都是1的data的可能性会比class 1要大 Naive bayes认为从class 2中找到样本点x的概率是x中第一个feature出现的概率与第二个feature出现的概率之积：$P(x|C_2)=P(x_1=1|C_2)\cdot P(x_2=1|C_2)$；但是我们的直觉告诉自己，两个feature之间肯定是有某种联系的，$P(x|C_2)$不能够那么轻易地被拆分成两个独立的概率乘积，也就是说Naive bayes自作聪明地多假设了一些条件所以，==**Generative model和discriminative model的差别就在于，Generative的model它有做了某些假设，假设你的data来自于某个概率模型；而Discriminative的model是完全不作任何假设的**== Generative model做的事情就是脑补，它会自己去想象一些事情，于是会做出一个和我们人类直觉想法不太一样的判断结果，就像toy example里，我们做了naive bayes这样一个假设(事实上我们并不知道这两个feature是否相互独立)，于是Naive bayes会在class 2里并没有出现过两个feature都是1的样本点的前提下，自己去脑补有这样的点通常脑补不是一件好的事情，因为你给你的data强加了一些它并没有告诉你的属性，但是在data很少的情况下，脑补也是有用的，discriminative model并不是在所有的情况下都可以赢过Generative model，discriminative model是十分依赖于data的，当data数量不足或是data本身的label就有一些问题，那Generative model做一些脑补和假设，反而可以把data的不足或是有问题部分的影响给降到最低在Generative model中，priors probabilities和class-dependent probabilities是可以拆开来考虑的，以语音辨识为例，现在用的都是neural network，是一个discriminative的方法，但事实上整个语音辨识的系统是一个Generative的system，它的prior probability是某一句话被说出来的几率，而想要estimate某一句话被说出来的几率并不需要有声音的data，可以去互联网上爬取大量文字，就可以计算出某一段文字出现的几率，并不需要声音的data，这个就是language model，而class-dependent的部分才需要声音和文字的配合，这样的处理可以把prior预测地更精确 #### Conclusion 对于分类的问题(主要是二元分类)，我们一般有两种方法去处理问题，一种是Generative的方法，另一种是Discriminative的方法，注意到分类问题的model都是从贝叶斯方程出发的，即 $$ \begin{split} P(C_i|x)&=\frac{P(C_i)P(x|C_i)}{\sum\limits_{j=1}^nP(C_j)P(x|C_j)} \ \ (1) \\ &=\sigma(z)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-(b+\sum\limits_k w_k x_k)}} \ \ (2) \end{split} $$ 其中分子表示属于第i类的可能性，分母表示遍历从1到n所有的类的可能性，两种方法的区别在于： Generative model会假设一个带参数的Probability contribute，利用这个假设的概率分布函数带入(1)中去计算$P(x|C_i)$和$P(x|C_j)$，结合极大似然估计法最终得到最优的参数以确定这个model的具体形式 DIscriminative model不作任何假设，因此它无法通过假定的Probability distribution得到$P(x|C_i)$的表达式，因此它使用的是(2)，直接去利用交叉熵和gradient descent结合极大似然估计法得到最优的b和w，以确定model的具体形式最后，利用得到的$P(C_i|x)$与0.5相比较来判断它属于那个class的可能性更大 Generative model的好处是，它对data的依赖并没有像discriminative model那么严重，在data数量少或者data本身就存在noise的情况下受到的影响会更小，而它还可以做到Prior部分与class-dependent部分分开处理，如果可以借助其他方式提高Prior model的准确率，对整一个model是有所帮助的(比如前面提到的语音辨识) 而Discriminative model的好处是，在data充足的情况下，它训练出来的model的准确率一般是比Generative model要来的高的 #### Multi-class Classification ##### softmax 之前讲的都是二元分类的情况，这里讨论一下多元分类问题，其原理的推导过程与二元分类基本一致假设有三个class：$C_1,C_2,C_3$，每一个class都有自己的weight和bias，这里$w_1,w_2,w_3$分布代表三个vector，$b_1,b_2,b_3$分别代表三个const，input x也是一个vector > softmax的意思是对最大值做强化，因为在做第一步的时候，对$z$取exponential会使大的值和小的值之间的差距被拉得更开，也就是强化大的值我们把$z_1,z_2,z_3$丢进一个**softmax**的function，softmax做的事情是这样三步： * 取exponential，得到$e^{z_1},e^{z_2},e^{z_3}$ * 把三个exponential累计求和，得到total sum=$\sum\limits_{j=1}^3 e^{z_j}$ * 将total sum分别除去这三项(归一化)，得到$y_1=\frac{e^{z_1}}{\sum\limits_{j=1}^3 e^{z_j}}$、$y_2=\frac{e^{z_2}}{\sum\limits_{j=1}^3 e^{z_j}}$、$y_3=\frac{e^{z_3}}{\sum\limits_{j=1}^3 e^{z_j}}$

原来的output z可以是任何值，但是做完softmax之后，你的output $y_i$的值一定是介于0~1之间，并且它们的和一定是1，$\sum\limits_i y_i=1$，以上图为例，$y_i$表示input x属于第i个class的概率，比如属于C1的概率是$y_1=0.88$，属于C2的概率是$y_2=0.12$，属于C3的概率是$y_3=0$ 而softmax的output，就是拿来当z的posterior probability 假设我们用的是Gaussian distribution(共用covariance)，经过一般推导以后可以得到softmax的function，而从information theory也可以推导出softmax function，[Maximum entropy](https://en.wikipedia.org/wiki/Maximum_entropy)本质内容和Logistic Regression是一样的，它是从另一个观点来切入为什么我们的classifier长这样子 ##### multi-class classification的过程：如下图所示，input x经过三个式子分别生成$z_1,z_2,z_3$，经过softmax转化成output $y_1,y_2,y_3$，它们分别是这三个class的posterior probability，由于summation=1，因此做完softmax之后就可以把y的分布当做是一个probability contribution，我们在训练的时候还需要有一个target，因为是三个class，output是三维的，对应的target也是三维的，为了满足交叉熵的条件，target $\hat{y}$也必须是probability distribution，这里我们不能使用1,2,3作为class的区分，为了保证所有class之间的关系是一样的，这里使用类似于one-hot编码的方式，即 $$ \hat{y}= \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix}_{x \ ∈ \ class 1} \hat{y}= \begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix}_{x \ ∈ \ class 2} \hat{y}= \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}_{x \ ∈ \ class 3} $$

这个时候就可以计算一下output $y$和 target $\hat{y}$之间的交叉熵，即$-\sum\limits_{i=1}^3 \hat{y}_i \ln y_i$，同二元分类一样，多元分类问题也是通过极大似然估计法得到最终的交叉熵表达式的，这里不再赘述 ##### Limitation of Logistic Regression Logistic Regression其实有很强的限制，给出下图的例子中的Training data，想要用Logistic Regression对它进行分类，其实是做不到的

因为Logistic Regression在两个class之间的boundary就是一条直线，但是在这个平面上无论怎么画直线都不可能把图中的两个class分隔开来 ##### Feature Transformation 如果坚持要用Logistic Regression的话，有一招叫做**Feature Transformation**，原来的feature分布不好划分，那我们可以将之转化以后，找一个比较好的feature space，让Logistic Regression能够处理假设这里定义$x_1'$是原来的点到$\begin{bmatrix}0\\0 \end{bmatrix}$之间的距离，$x_2'$是原来的点到$\begin{bmatrix}1\\ 1 \end{bmatrix}$之间的距离，重新映射之后如下图右侧(红色两个点重合)，此时Logistic Regression就可以把它们划分开来

但麻烦的是，我们并不知道怎么做feature Transformation，如果在这上面花费太多的时间就得不偿失了，于是我们会希望这个Transformation是机器自己产生的，怎么让机器自己产生呢？==**我们可以让很多Logistic Regression cascade(连接)起来**== 我们让一个input x的两个feature $x_1,x_2$经过两个Logistic Regression的transform，得到新的feature $x_1',x_2'$，在这个新的feature space上，class 1和class 2是可以用一条直线分开的，那么最后只要再接另外一个Logistic Regression的model(对它来说，$x_1',x_2'$才是每一个样本点的"feature"，而不是原先的$x_1,x_2$)，它根据新的feature，就可以把class 1和class 2分开

因此着整个流程是，先用n个Logistic Regression做feature Transformation(n为每个样本点的feature数量)，生成n个新的feature，然后再用一个Logistic Regression作classifier Logistic Regression的boundary一定是一条直线，它可以有任何的画法，但肯定是按照某个方向从高到低的等高线分布，具体的分布是由Logistic Regression的参数决定的，每一条直线都是由$z=b+\sum\limits_i^nw_ix_i$组成的(二维feature的直线画在二维平面上，多维feature的直线则是画在多维空间上) 下图是二维feature的例子，分别表示四个点经过transform之后的$x_1'$和$x_2'$，在新的feature space中可以通过最后的Logistic Regression划分开来

注意，这里的Logistic Regression只是一条直线，它指的是“属于这个类”或“不属于这个类”这两种情况，因此最后的这个Logistic Regression是跟要检测的目标类相关的，当只是二元分类的时候，最后只需要一个Logistic Regression即可，当面对多元分类问题，需要用到多个Logistic Regression来画出多条直线划分所有的类，每一个Logistic Regression对应它要检测的那个类 ##### Powerful Cascading Logistic Regression 通过上面的例子，我们发现，多个Logistic Regression连接起来会产生powerful的效果，==**我们把每一个Logistic Regression叫做一个neuron(神经元)，把这些Logistic Regression串起来所形成的network，就叫做Neural Network，就是类神经网路，这个东西就是Deep Learning！**==