EverydayOneCat
久违的每日一喵去ヾ(≧▽≦*)o

Review
在宝可梦例子中,我们机器学习第三步优化用到了梯度下降法Gradient Descent
Example: θ have two variables {θ1,θ2}
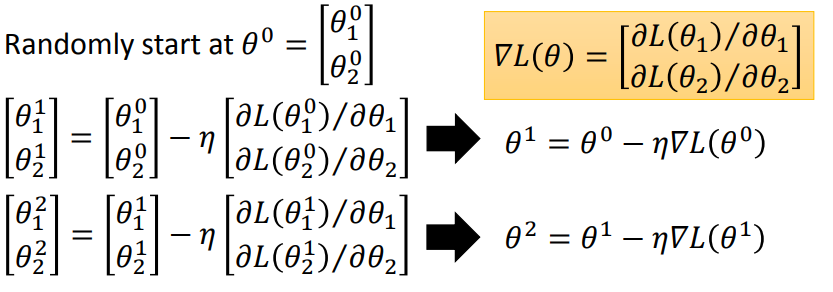
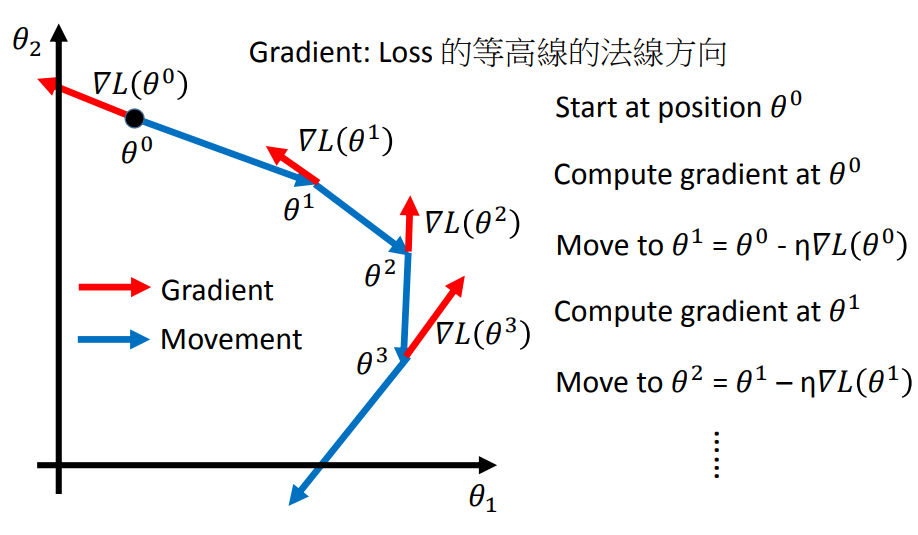
逐步优化θ1,θ2的值知道梯度为0为止。
在整个gradient descent的过程中,梯度不一定是递减的(红色箭头的长度可以长短不一),但是沿着梯度下降的方向,函数值loss一定是递减的,且当gradient=0时,loss下降到了局部最小值,总结:梯度下降法指的是函数值loss随梯度下降的方向减小。
Tuning Learning rate
Learning rate存在的问题
当我们用梯度下降法时,我们需要定义一个超参数Learning rate,而Learning rate的取值很有讲究,大致分为以下四种情况:
- 如果Learning rate正正好,那就可以像下图中红色线一样顺利到达loss最小值
- 如果Learning rate偏小,那么学习速度就会慢很多,最后虽然会走到loss最小值,但是走得非常慢,就和图中蓝色线段一样
- 如果Learning rate偏大,那么每次走的步伐就会变大,可能如图中绿色线一样跨国最小值然后左右徘徊
- 如果Learning rate很大,那么会直接飞出去,loss值不减反增,变得非常大
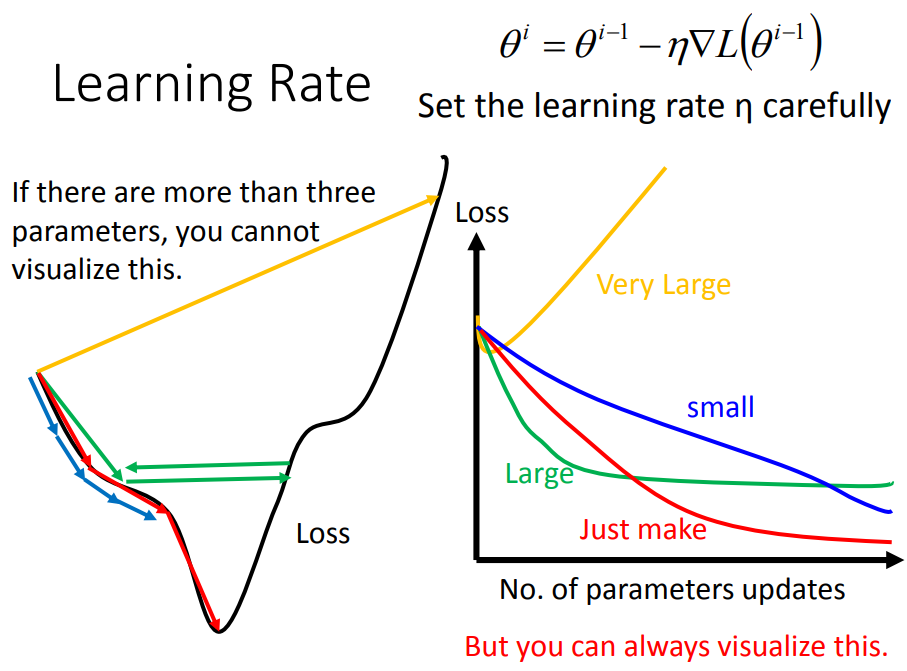
所以做gradient descent一个很重要的事情是,要把不同的learning rate下,loss随update次数的变化曲线给可视化出来,它可以提醒你该如何调整当前的learning rate的大小,直到出现稳定下降的曲线。
Adaptive Learning rates
当然,用可视化来改变Learning rate值是很麻烦的,所以我们通常采取一个最基本、最简单的原则来自动调整Learning rate:
Learning rate的大小通常是随着update的次数越来越小的。
Example:$η^t = \frac{η}{\sqrt{t+1}}$
上述例子是每个参数都以同样的方式随着update的次数减小,但是最好的状况是每个参数都给他不同的learning rate去update。
Adagrad
Adagrad就是将不同参数的learning rate分开考虑的一种算法(adagrad算法update到后面速度会越来越慢,当然这只是adaptive算法中最简单的一种)
定义超参数和梯度:$η^t = \frac{η}{\sqrt{t+1}}$ $g^t = \frac{d(L)}{d(w)}$(t表示第几次update,$σ^t$是之前所有Loss对w偏微分的方均根(根号下的平方均值))
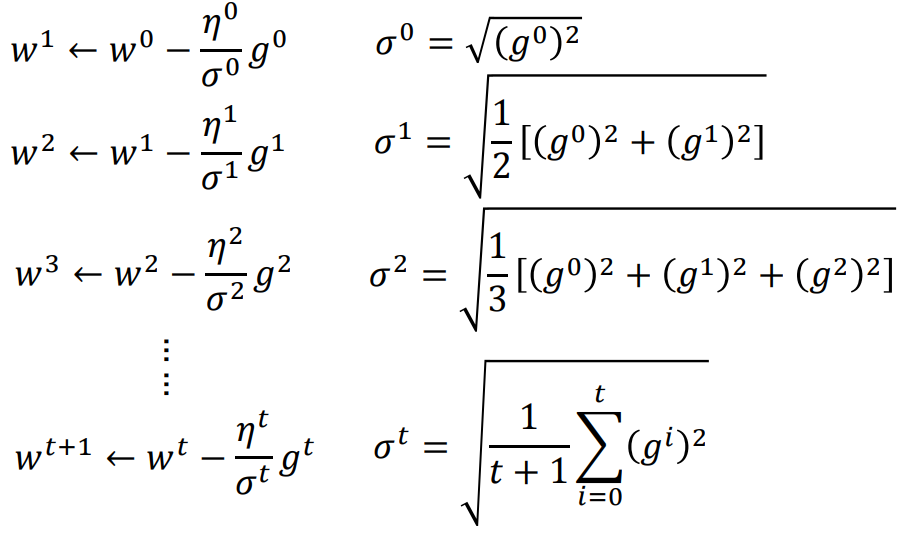
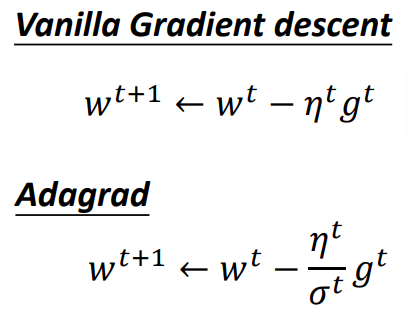
由于$η^t$和$σ^t$都有相同的因子$\sqrt{t+1}$可以相消,我们可以得到adagrad最终表达式
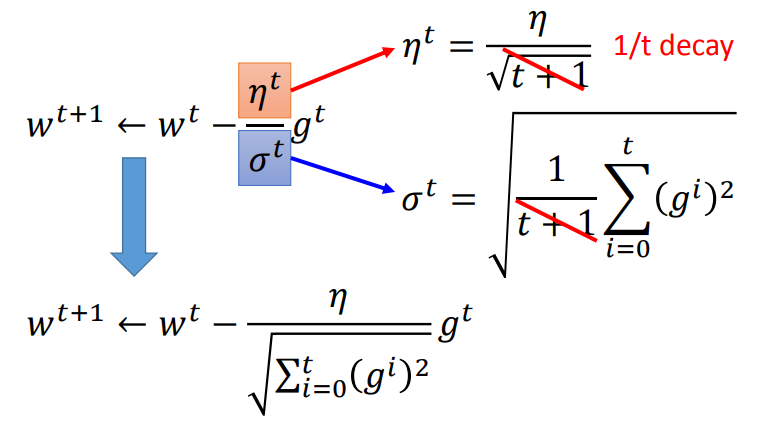
上面的最终表达式有一个很矛盾的地方,当梯度$g^t$越大时,我们想要迈的步子越大,但是在adagrad表达式中,分母则表示梯度越大迈的步子越小,似乎互相矛盾。其实Adagrad要考虑的是,这个gradient有多surprise,即反差有多大。

Other tips of gradient descent
Stochastic Grandient Descent
随机梯度下降的方法可以让训练更快速,传统的gradient descent的思路是看完所有的样本点之后再构建loss function,然后去update参数;而stochastic gradient descent的做法是,看到一个样本点就update一次,因此它的loss function不是所有样本点的error平方和,而是这个随机样本点的error平方。

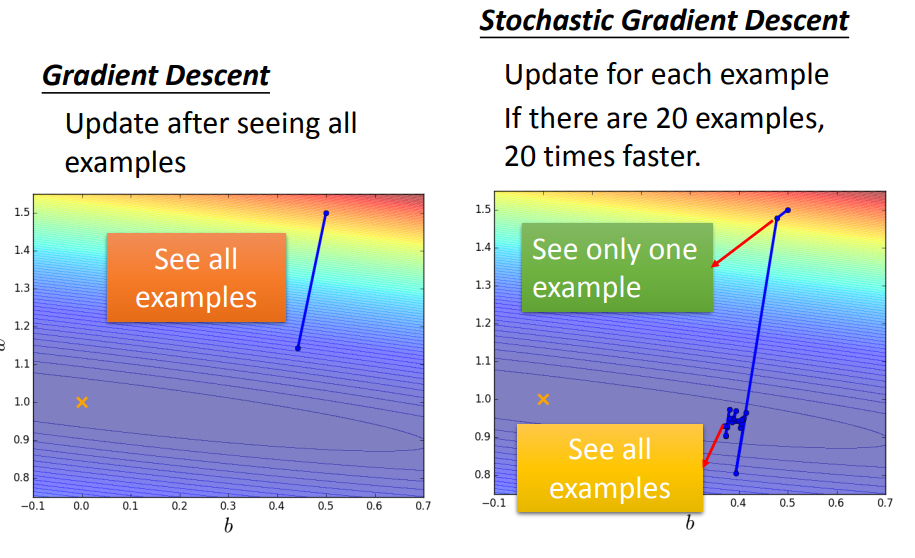
Feature Scaling
特征缩放:当多个特征分布范围不一样时,最好将这些不同的feature的范围缩放成一样。
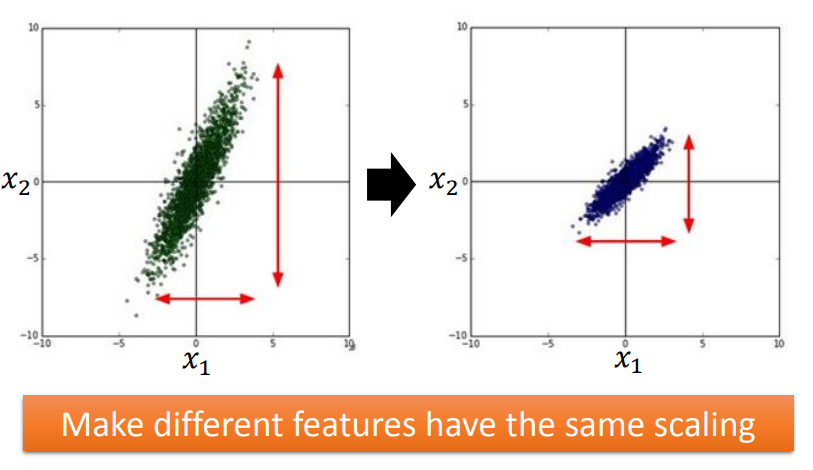
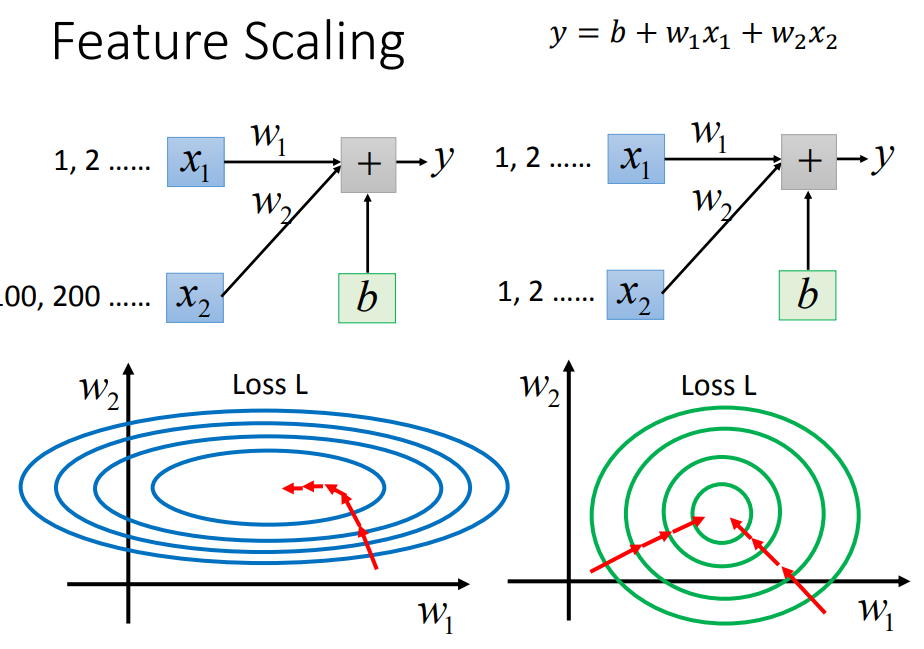
左边的error surface表示,w1对y的影响比较小,所以w1对loss是有比较小的偏微分的,因此在w1的方向上图像是比较平滑的;w2对y的影响比较大,所以w2对loss的影响比较大,因此在w2的方向上图像是比较sharp的。
如果x1和x2的值,它们的scale是接近的,那么w1和w2对loss就会有差不多的影响力,loss的图像接近于圆形。
如果有scale的话,loss在参数w1、w2平面上的投影就是一个正圆形,update参数会比较容易而且gradient descent的每次update并不都是向着最低点走的,每次update的方向是顺着等高线的方向(梯度gradient下降的方向),而不是径直走向最低点;但是当经过对input的scale使loss的投影是一个正圆的话,不管在这个区域的哪一个点,它都会向着圆心走。因此feature scaling对参数update的效率是有帮助的。
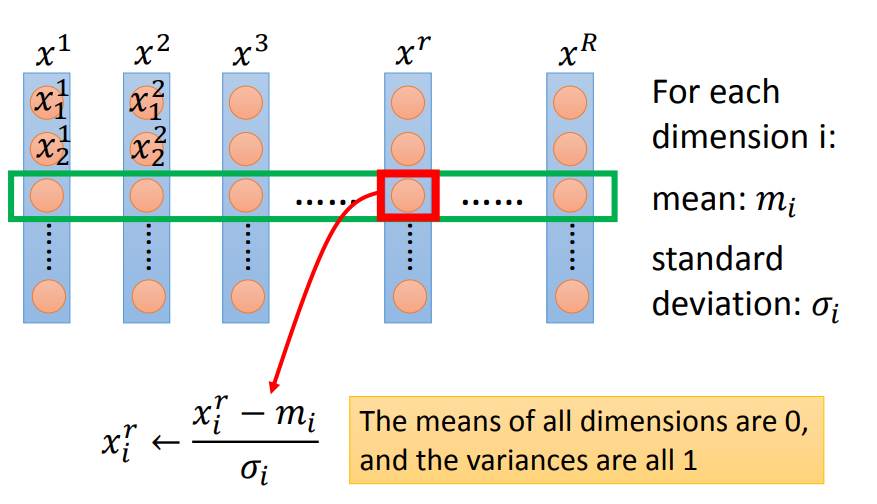
如何做Feature scaling:
对每一个demension i,都去算出它的平均值mean=$m_i$以及标准差standard deviation=$σ_i$
Gradient Descent的限制
gradient descent有一个问题是它会停在local minima的地方就停止update了
事实上还有一个问题是,微分值是0的地方并不是只有local minima,settle point的微分值也是0
以上都是理论上的探讨,到了实践的时候,其实当gradient的值接近于0的时候,我们就已经把它停下来了,但是微分值很小,不见得就是很接近local minima,也有可能像下图一样在一个高原的地方
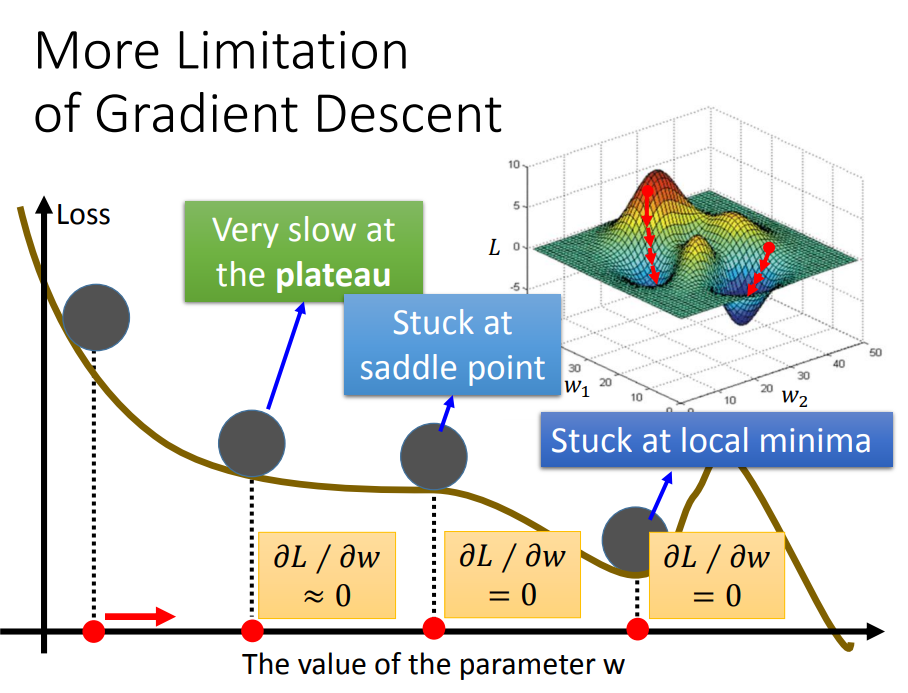
gradient descent的限制是,它在gradient即微分值接近于0的地方就会停下来,而这个地方不一定是global minima,它可能是local minima,可能是saddle point鞍点,甚至可能是一个loss很高的plateau平缓高原。


