写在前面
距离上次写学习笔记差不多已经一年半了,可恶,还差一年鼠鼠我就可以当练习生了耶😭
直到上了研究生才发现和本科区别不是很大,可能有还是研一的缘由,还有可能是我导师太忙管不到我的缘由,大部分知识还是要自己学的,目前已知的信息就是未来的两大研究方向都和机器学习有关,所以咱们博客复出的开篇就是机器学习入门系列,希望研究生的两年半能很好的提升自己吧😁。
ML的三大步骤
我们通过预测宝可梦进化后的cp值举例。
1.确定Model
即定义一个函数f,使得输出出来的结果和真正的结果近似最好是相等。这里并没有明确的思路,只能凭经验去尝试,我们从最简单的线性模型开始。
w和b是未知值,可以取任意值,而上述式子抽象出来即叫做Model。
上面的式子只考虑了进化前的cp值,而进化前我们还有很多因素可以考虑,因此我们可以写一个更复杂的线性模型:
参数描述:y——进化后cp预测值;b:bais;Xi:进化前的属性;wi:属性的权重

2.Define Loss
我们确定好model后需要定义一个评估函数来决定模型的好坏,通常称之为Loss Function,在这个例子里,我们可以这样写:
因为我们的模型输出y是由w和b决定的,因此Loss函数的input也是w和b,也就是说,Loss function其实是在评估一组参数的好坏。
参数说明:
Loss Function和Model一样也是我们自己来定义的,通常我们用方差的形式来衡量,即预测值和真值之间的差的平方和
由式子我们可以看出Loss越大,说明参数越不好。
我们可以通过Loss function的可视化来清晰的选出最好的w和b。下图(b,w)的每个点的像素颜色代表loss的大小,越红loss越大,越蓝越小,我们可以看出画叉的那个点的(b,w)是Loss最小的。

3.优化
第二步做完,我们已经确定好了我们的Loss function,接下来就是优化找到一个最好的模型function,其实就是找到使得L(f)=L(w,b)最小的那个w 和 b。
这里介绍一种普遍的方法——gradient descent(梯度下降法)。
Gradient descent
gradient descent的厉害之处在于,只要L(f)是可微分的,gradient descent都可以拿来处理这个f,找到表现比较好的parameters。
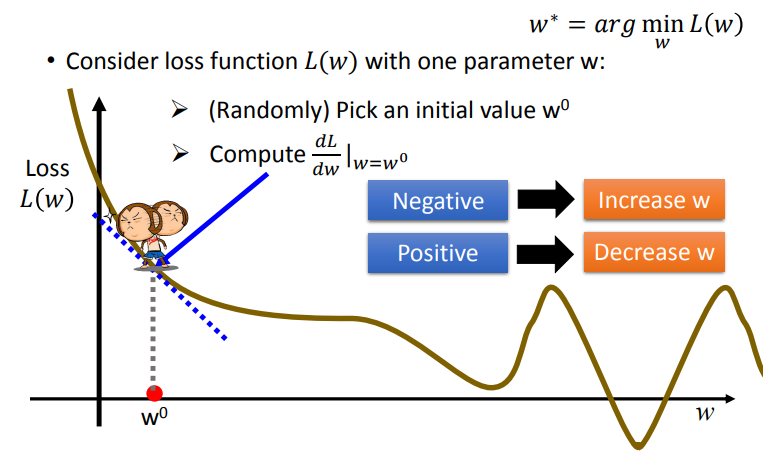
我们举个单参数的例子L(w),我们的目标就是要找到使得L最小的参数w*。
梯度下降法分为以下几步:
首先随机选取一个点wo
计算函数在该点的微分,若是负的,说明左大右小,应使得w变大;;若是正的,应使得w变小
w的改变量step size不止决定于该点的微分,还决定于一个超参数η,我们成为learning rate,如果η越大,那么w每次移动的步幅也就越大,反之也越小。
如果learning rate设置的大一点,那么也就代表着机器学习的速度快一点,但是有可能导致步子迈大了错过了最合适的全局最小的点。
当斜率为0时,即找到一个极小值,但是我们观察下图,会发现有找到极小值但是不是全局最小值的现象。这种问题我们在线性模型里其实并不用担心,因为在线性模型中我们的Loss function其实是个convex,就是凸函数,他只有一个global minima全局最优解。
评估系统
回到我们的例子来,我们在loss function中定义了两个参数L(w,b),其实本质上和单参数问题是一样的解决方法,只不过微分变味了偏微分。
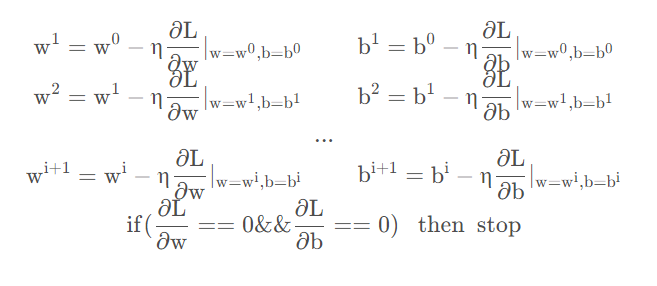
用梯度下降法我们可以得到最好的参数是b=-188.4, w=2.7
我们需要一套评估系统来观测我们预测的值和实际值的误差error的大小,这里又分为训练数据和测试数据的误差。
training data里得到的误差一般是要比testing data要小,这也符合常识,当然我们实际关心的就是测试数据的数据(训练没见过的数据)。
重新设计模型
实际上,从结果来看,最终的function可能不是一条直线,可能是稍微更复杂一点的曲线,我们考虑二次方的model,即
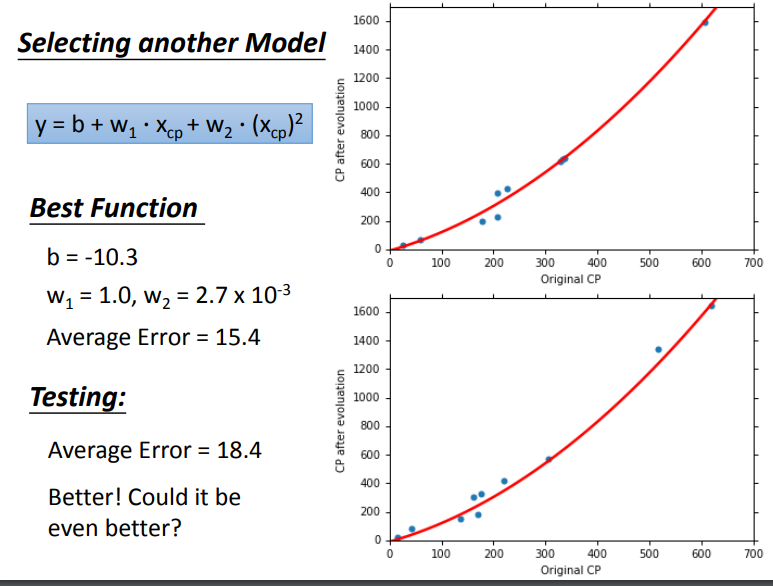
考虑三次方的model:
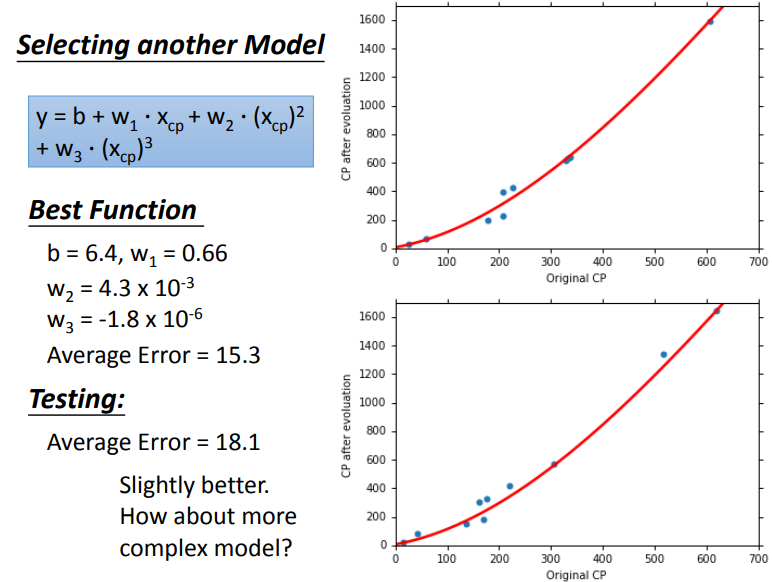
考虑四次方的model:
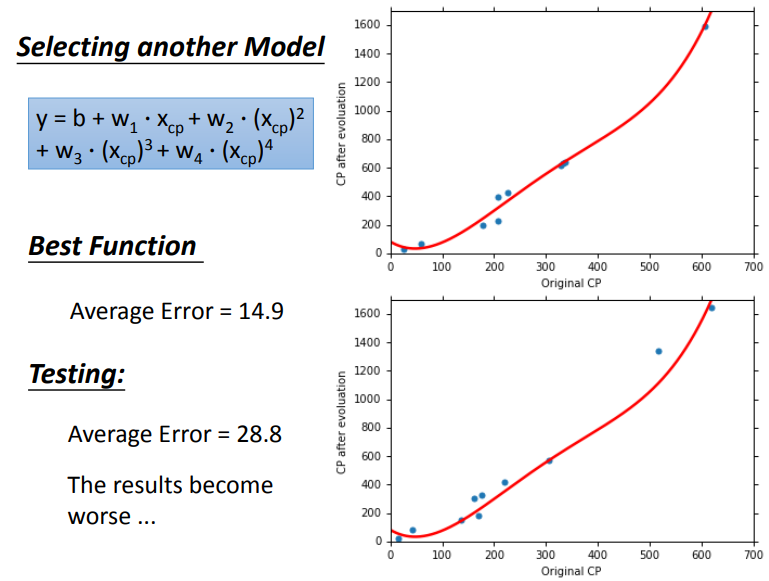
考虑五次方:

我们由上述五个model的表现可以观测出:
随着高次项的增加,训练数据的average error会逐渐减少,但是这不是我们关心的,我们发现在测试数据上,model复杂到一定程度后,error不减反增,这种现象,我们称之为过拟合overfitting。

因此不是model越复杂越好,我们需要选一个最合适的model。
引入更多参数
我们收集更多数据放入training data,发现进化前后的cp值还与种族有关联,记种族为Xs。

重新设计model: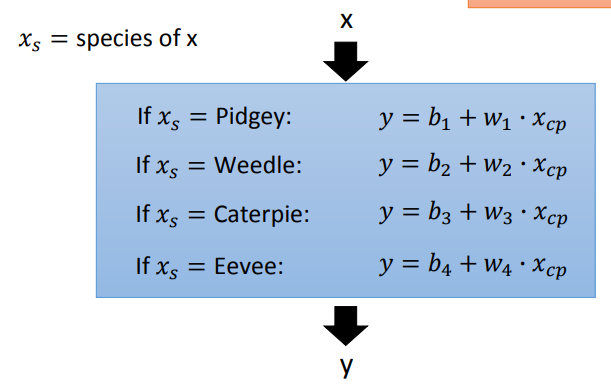
这里引入δ(条件表达式)的概念,当条件表达式为true,则δ为1;当条件表达式为false,则δ为0,因此可以通过下图的方式,将4个if语句转化成同一个linear model

我们发现引入种族Xs后,training error和testing error都明显下降:
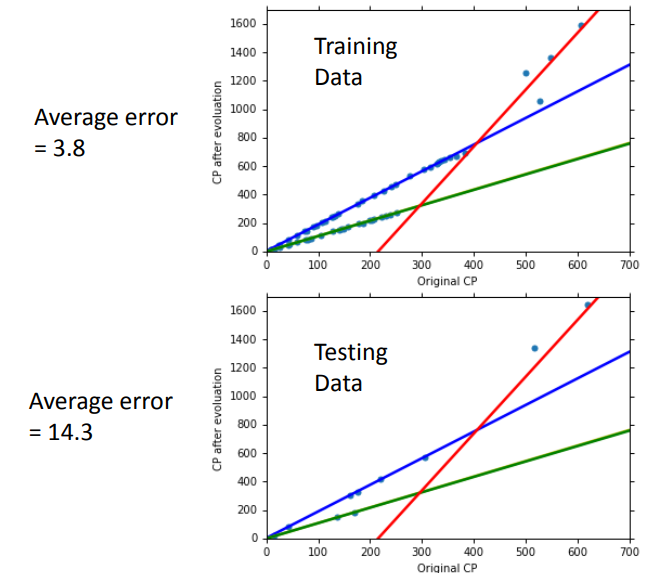
接着我们观测是不是参数考虑得越多越好,我们将可能的参数都引入,设计出一个最复杂的model:

我们发现模型设计的复杂反而更容易造成overfitting现象。
正则化解决过拟合问题
Regularization可以使得曲线变得更加平滑,使得training data 上的error变大,testing data上的error变小。
在之前的Loss function中我们只考虑了预测值的error,即
而Regularization则是在这个基础上加上λ ∑ ( w i ) 2 ,即
而平滑的意思就是wi要尽可能的小即趋向于0,为什么呢?
因为当我们的function对input越不敏感,说明这个function越平滑,当我们的参数wi趋向于0时,output对input的输入是不敏感的。而我们不考虑把bais放进入的原因是bais与function的平滑度没有关系,它的作用只是把function上下移动而已。
那为什么我们喜欢平滑的function呢?
因为当我们对input不敏感时,一些noise噪声对我们的预测值影响不算很大,会给一个比较好的结果。
而λ则需要我们手动去调整以取得最好的值,当λ设定的越大,我们找到的function就越平滑。
观察下图可知,当我们的λ越大的时候,在training data上得到的error其实是越大的,但是这件事情是非常合理的,因为当λ越大的时候,我们就越倾向于考虑w的值而越少考虑error的大小;但是有趣的是,虽然在training data上得到的error越大,但是在testing data上得到的error可能会是比较小的。
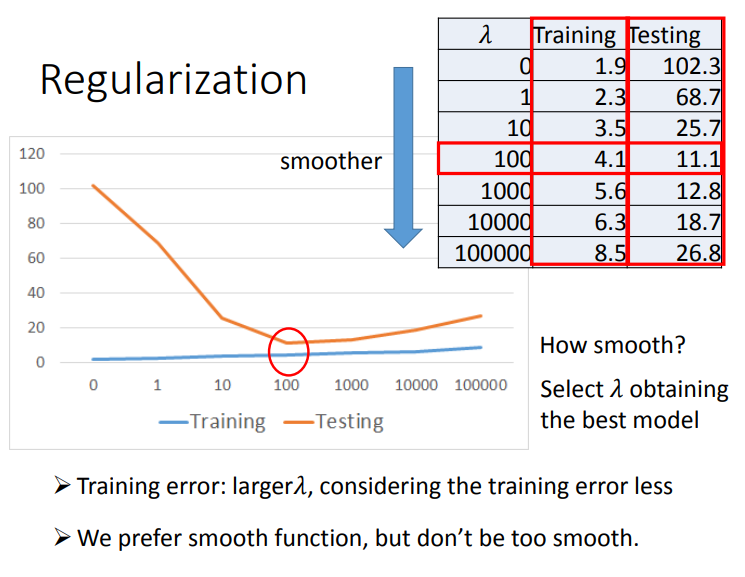
我们喜欢比较平滑的function,因为它对noise不那么sensitive;但是我们又不喜欢太平滑的function,因为它就失去了对data拟合的能力;而function的平滑程度,就需要通过调整λ来决定。
Error
error的来源
error from testing data 来源于两个方向:bais和variance
通常我们可以通过一堆training data分组来确定多个$ f^ $,对这些$ f^ $取平均我们可以得到$\overline{f}$
由下图我们可以观测到,如果bais造成的误差越大,那么我们定义的function离真正正确的model就越远,而variance造成的误差越大,说明我们确定的多个$ f^* $越离散。

对上面宝可梦的例子,我们训练1000条数据,把1000条分为100组,确定不同的$ f^* $,用图像直观的展示出来。

我们可以简单地观测出一个结论:当模型越简单,方差越小,可以看到function基本都集中起来,但是简单模型往往平均起来很偏移正确的model;而当模型越复杂,方差就会随之变大,fucntion也很离散,但是他们的平均往往和正确的model很接近。
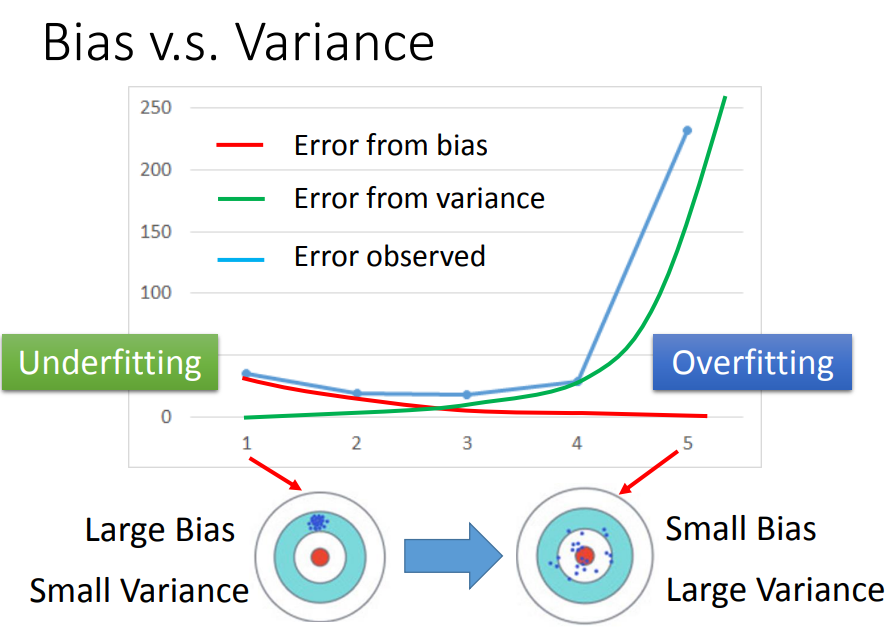
解决error的方法
一般情况下,我们会出现两种问题:
- 如果你的model并不能fit训练集,那这个model有很大的bais——欠拟合问题
- 如果你的model能fit训练集,但是在测试集上有很大的error,那model有很大的variance——过拟合问题
对于欠拟合问题,我们解决方法通常有两种:
- 引入更多的object的属性变量
- 重新定义一个更复杂的model
对于过拟合问题,我们解决方法也有两种:
- 收集更多的training data
- 正则化解决过拟合问题
在实际的选择模型中,我们在往往采用n重交叉验证的方式,这样得到的function往往具有良好的泛化能力。

结语
骚话想不出来了,老了呀😭


