左神数据结构和算法（基础）

1.简单排序算法

异或方法交换两值

一个很有意思不需要开辟新缓冲的方法——通过异或运算实现两数交换

首先我们需要了解异或的性质：

1. a^0 = a a^a=0
2. 满足交换律和结合律

//三轮a异或b实现两数交换
public static void swap(int[] arr,int i,int j){
    arr[i]= arr[i]^arr[j];
    arr[j]=arr[i]^arr[j];
    arr[i]=arr[i]^arr[j];
}

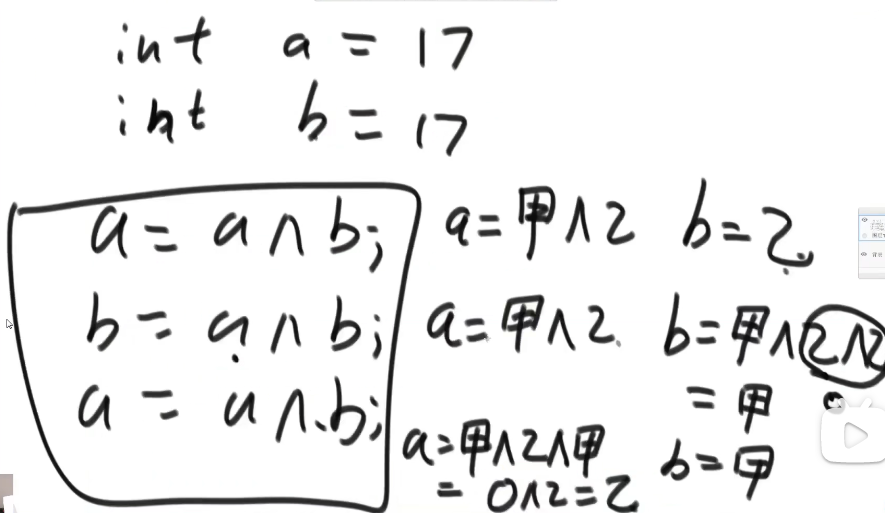
这里a和b必须满足两者指向两块不同的内存区域，否则这种方法会使两值都变为0

异或思考题

要求：时间复杂度O(n)；空间复杂度O(1)

在数组arr中

（1）有一种数出现了奇数次，其余都是偶数次，如何找到这个数

解析：定义一个数eor=0，将其和数组中所有数异或得到的数即为奇数次的这个数。

public int questionOne(int[] arr){
    int result = arr[0];
    for(int i=1;i<arr.length;i++){
        result = result^arr[i];
    }
    return result;
}

（2）有两种数出现了奇数次，其余都是偶数次，如何找到这两个数

解析：设数组中奇数次数是a和b，定义eor=0，将其和数组所有元素异或后得到eor=a^b

由于a!=b，所以eor至少有一位不为0，说明a和b有一位不一样

假设第8位不一样，将数组中的元素按照第八位是0或1分为两组，a和b肯定分别在这两个组中

定义eor’遍历异或其中一组即得到a或者b，接着eor^eor’即得到另一个数

public void questionTwo(int []arr){
    int eor = 0;
    for (int index:arr){
        eor ^=index;
    }
    //得到eor=a^b
    //eor至少有一位不为0

    int rightOne = eor & (~eor+1);//按位提取最右的1,其余位都为0

    int onlyOne = 0;
    for (int cur:arr){
        if((cur&rightOne)==0){//只和一组异或
            onlyOne ^=cur;
        }
    }
    System.out.println("奇数次的两个数分别为"+onlyOne+"和"+(eor^onlyOne));
}

选择、冒泡、插入排序

选择排序：时间复杂度O(n^2) 空间复杂度O(1)

public void selectionSort(int[] arr){
    //合法性判断
    if(arr==null||arr.length<2){
        return;
    }
    for (int i = 0;i<arr.length-1;i++){
        int minIndex = i;//默认i号元素最小
        for(int j=i+1;j<arr.length;j++){
            minIndex = arr[j]>arr[minIndex]?minIndex:j;
        }
        if(minIndex!=i) {
            Swap.swap(arr,i,minIndex);
        }
    }
}

冒泡排序 时间复杂度O(n^2) 空间复杂度O(1)

public void bubbleSort(int[] arr){
    //合法性判断
    if(arr==null||arr.length<2){
        return;
    }
    for(int i=arr.length;i>0;i--){
        for (int j = 0; j < i-1; j++) {
            if(arr[j]>arr[j+1]){
                Swap.swap(arr,j,j+1);
            }
        }
    }
}

插入排序和数组顺序有关，最好的情况下时间复杂度O(n),最坏的情况下则是O(n^2)，因此插入排序比冒泡和选择排序要好一点

public void insertionSort(int []arr){
    //合法性判断
    if(arr==null||arr.length<2){
        return;
    }
    for (int i = 1; i <arr.length ; i++) {//实现0~i有序
        for (int j = i-1; j>=0&&arr[j]>arr[j+1] ; j--) {
            Swap.swap(arr,j,j+1);
        }
    }
}

2.O(logn)的排序

master公式

题目：求出一个数组中元素的最大值

public int araayGetMax(int[] arr){
    return getMax(arr,0,arr.length-1);
}

//求[L,R]上最大值
public int getMax(int[] arr,int L,int R){
    if(L==R){
        return arr[L];
    }
    //找出中间点
    /*这里有一个知识点：我们求中间点可以用(L+R)/2来得到，但是存在一个安全隐患：L+R可能会溢出
        * 我们可以用L+(R-L)/2同样求出中间点，其中/2操作可以看成右移一位（位运算快得多）
        * */
    int mid = L + ((R-L)>>1);
    //递归
    int leftMax = getMax(arr,L,mid);
    int rightMax = getMax(arr,mid+1,R);
    return Math.max(leftMax,rightMax);
}

这种运用了递归的算法我们求时间复杂度时，我们通常用到master公式

master公式： T(n) = a * T(N/b) + O(N^d);

当：

log b A < d 时，程序的时间复杂度为：O(N^d);

log b A > d 时，程序的时间复杂度为：O(N^log b A);

log b A = d 时，程序的时间复杂度为：O(N^d * log N);

符合子问题规模是等规模的行为，均可使用master公式求解时间复杂度。

如上述程序我们在求一个数组长度为N的最大值时，其中

a: 子问题调用的次数，本程序的次数为2次（leftMax和rightMax）；

N：为母问题规模，本程序的母问题规模为N；

T(N/b): 子问题规模，本程序的子问题规模为：N/2（二分）；

O(n^d)： 除子问题调用之外的时间复杂度，本程序为O(1)；

可得本程序的master公式为：T(N) = 2 * T(N/2) + O(1);其中a=2,b=2,d=0

所以，本程序的时间复杂度为：O(N)

归并排序

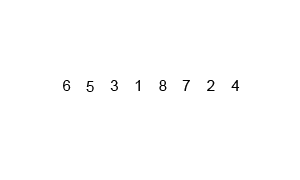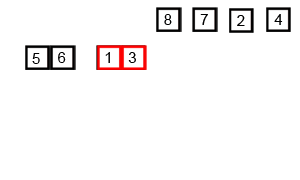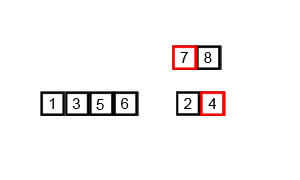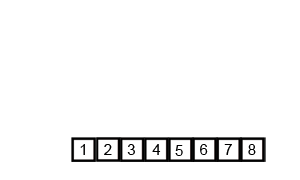
public void mergeSort(int[] arr){
    //合法性判断
    if(arr==null||arr.length<2){
        return;
    }
    process(arr,0,arr.length-1);
}

//将L到R排好序
public void process(int[] arr,int L,int R){
    if(L==R){
        return;
    }
    //求出中点
    int mid = L + ((R-L)>>1);
    //数组分为左右两部分
    process(arr,L,mid);//先把左边排好序
    process(arr,mid+1,R);//再把右边排好序
    //合并左右两边
    merge(arr,L,mid,R);
}

private void merge(int[] arr, int L, int mid, int R) {
    //创造辅助数组
    int[] help = new int[R-L+1];
    int i = 0;
    //p1,p2为左右两部分的索引
    int p1= L;
    int p2= mid+1;
    while(p1<=mid&&p2<=R){
        help[i++] = (arr[p1]<=arr[p2])?arr[p1++]:arr[p2++];
    }
    while(p1<=mid){
        help[i++] = arr[p1++];
    }
    while (p2<=R){
        help[i++] = arr[p2++];
    }
    for (int j = 0; j < help.length; j++) {
        arr[L+j] = help[j];
    }
}

分析时间复杂度，子问题等规模，可以用master公式：T(N) = a*T(N/b) + O(N^d)

此处master公式为：T(N) = 2T(N/2) + O(N)，其中a=2,b=2,d=1，因此时间复杂度是O(N\logN)

小和问题

在一个数组中，每一个元素左边比当前元素值小的元素值累加起来，叫做这个数组的小和
例如：[2,3,4,1,5]
2左边比2小的元素：无
3左边比3小的元素：2
4左边比4小的元素：2，3
1左边比1小的元素：无
5左边比5小的元素：2,3,4,1
小和small_sum = 2 + 2 + 3 + 2 + 3 + 4 + 1 = 17

分析：

上述举例可以转化成该元素右边有多少比自己大的元素的个数，小和=每个元素数值*每个元素求出的这个个数。

如上述例子中，2右边比它大的元素有3个，3右边有2个，4右边有1个，1右边有一个，5右边没有，最终小和=2*3+3*2+4+1=17

我们可以用归并排序的特点来解决此问题，小和只有在merge的过程中才会产生，并且小和只有在左边的数字小于右边的数字的时候才会产生小和，因为在merge过程中，左右两边已经有序，所以在本次merge过程中该数字产生小和的个数可以用下标计算得出。一个有序数组内不产生任何小和（因为我们已经在之前的merge过程中计算过了）。这样做我们就不会把小和重复计算。

public int smallSum(int[] arr){
    return process(arr,0,arr.length-1);
}

//    [L,R]既要排好序，又要求小和
public int process(int[] arr,int L,int R){
    if(L==R){
        return 0;
    }
    int mid = L + ((R-L)>>1);

    return process(arr,L,mid) + process(arr,mid+1,R) + merge(arr,L,mid,R);

}

private int merge(int[] arr, int L, int mid, int R) {
    int[] help = new int[R-L+1];
    int sum = 0;
    int i = 0;
    int p1=L;
    int p2=mid+1;
    while(p1<=mid&&p2<=R){
        sum += (arr[p1]<arr[p2])?arr[p1]*(R-p2+1):0;
        help[i++] = (arr[p1]<arr[p2])?arr[p1++]:arr[p2++];
    }
    while (p1<=mid){
        help[i++] = arr[p1++];
    }
    while(p2<=R){
        help[i++] = arr[p2++];
    }
    for (int j = 0; j < help.length; j++) {
        arr[L+j] = help[j];
    }
    return sum;
}

逆序对问题

在一个数组中，左边的数如果比右边的数大，则这两个数构成一个逆序对，请打印所有的逆序对。

public void reverseOrder(int[] arr){
    //合法性判断
    if(arr==null||arr.length<2){
        return;
    }
    process(arr,0,arr.length-1);
}

//打印[L,R]上所有的逆序对
public void process(int[] arr,int L,int R){
    if(L==R){
        return;
    }
    int mid = L + ((R-L)>>1);
    //打印左右两部分的逆序对
    process(arr,L,mid);
    process(arr,mid+1,R);
    //打印合并过程中的逆序对
    merge(arr,L,mid,R);
}

private void merge(int[] arr, int L, int mid, int R) {
    int[] help = new int[R-L+1];
    int i = 0;
    int p1=L;
    int p2=mid+1;
    while(p1<=mid&&p2<=R){
        if(arr[p1]>arr[p2]){
            for (int j = p1; j <=mid ; j++) {
                System.out.println("["+arr[j]+","+arr[p2]+"]");
            }
        }
        help[i++] = (arr[p1]>arr[p2])?arr[p2++]:arr[p1++];
    }
    while (p1<=mid){
        help[i++] = arr[p1++];
    }
    while(p2<=R){
        help[i++] = arr[p2++];
    }
    for (int j = 0; j < help.length; j++) {
        arr[L+j] = help[j];
    }
}

荷兰国旗问题

问题一：

给定一个数组arr，和一个数num，请把小于等于num的数放在数组的左边，大于num的数放在数组的右边。要求额外空间复杂度O(1)，时间复杂度O(N)

分析：

问题二：

给定一一个数组arr和一个数num，请把小于num的数放在数组的左边，等于num的数放在数组的中间，大于num的数放在数组的右边。要求额外空间复杂度O(1)，时间复杂度O(N)

快速排序

平均时间复杂度O(N*logN)，空间复杂度O(logN)

public void quickSort(int[] arr){
    //合法性判断
    if(arr==null||arr.length<2){
        return;
    }
    quickSort(arr,0,arr.length-1);
}

//[L,R上排好序]
public void quickSort(int[] arr,int L,int R){
    if(L<R){
        //任意一个数为基值
        swap(arr, L+(int)(Math.random()*(R-L+1)),R);
        int[] boundary = partition(arr,L,R);
        quickSort(arr,L,boundary[0]-1);
        quickSort(arr,boundary[1]+1,R);
    }
}


//默认以arr[R]做划分
//返回等于区域（左边界，右边界），返回一个长度为2的数组
/*荷兰国旗问题：
    * 当前值小于划分值，当前值和<区域的后一个值做交换，<区域右扩，i++
    * 当前值大于划分值，当前值和>区域的前一个值交换，>区域左扩，i不变
    * 当前值等于划分值，i++
    * */
private int[] partition(int[] arr, int L, int R) {
    int less = L-1; // <的右边界
    int more = R; // >的左边界
    //默认L表示当前数的位置
    while(L<more){
        if(arr[L]<arr[R]){//当前值小于划分值
            swap(arr,++less,L++);
        }else if(arr[L]>arr[R]){//当前值大于划分值
            swap(arr,--more,L);
        }else {
            L++;
        }
    }
    swap(arr,R,more);
    return new int[] {less+1,more};
}

3.堆排序和排序总结

堆排序

堆排序用到了大顶堆的概念，之前的博文中已经介绍，想看的朋友自行翻阅《堆，图，字符串匹配算法超详细讲解》这篇。

public void heapSort(int[] arr){
    //合法性判断
    if(arr==null||arr.length<2){
        return;
    }
    //        for (int i = 0; i < arr.length; i++) {
    //            heapInsert(arr,i);
    //        }
    for (int i = arr.length-1; i >=0 ; i--) {
        heapify(arr,i,arr.length);
    }
    int heapsize = arr.length;
    swap(arr,0,--heapsize);

    while (heapsize>0){//O(N)
        heapify(arr,0,heapsize);//O(logN)
        swap(arr,0,--heapsize);
    }
}

//大顶堆插入数据
public void heapInsert(int[] arr,int index){
    while(arr[index]>arr[(index-1)/2]){
        swap(arr,index,(index-1)/2);
        index = (index-1)/2;
    }
}

//从一个位置自上而下堆化
public void heapify(int []arr,int index,int heapsize){
    //左孩子的下标
    int left = index*2+1;
    while(left<heapsize){
        //左右孩子最大的下标
        int largest = (left+1<heapsize)&&arr[left+1]>arr[left]?left+1:left;
        //父节点和孩子节点比较
        largest = arr[largest]>arr[index]?largest:index;
        if(index == largest){
            return;
        }
        swap(arr,index,largest);
        index = largest;
        left = index*2+1;
    }
}

堆排序扩展题目

已知一个几乎有序的数组，几乎有序是指，如果把数组排好顺序的话，每个元素移动的距离可以不超过k，并且k相对于数组来说比较小。
请选择一个合适的排序算法针对这个数据进行排序。

分析

我们可以利用小顶堆来进行排序，假设k=6，我们一开始先将数组下标为0~6的元素放入小顶堆，小顶堆弹出的第一个元素就是最小的数放入0位置（由于最大距离为6，因此最小的肯定是数组中最小的），接着将7号元素放入小顶堆，小顶堆弹出的放入1号位置，循环往复…………

public void process(int[] arr,int k){
    //优先级队列就是由小顶堆实现的
    PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
    int index = 0;
    for(;index<Math.min(arr.length,k);index++){
        priorityQueue.add(arr[index]);
    }
    int i = 0;
    for(;index<arr.length;i++,index++){
        priorityQueue.add(arr[index]);
        arr[i] = priorityQueue.poll();
    }
    while(!priorityQueue.isEmpty()){
        arr[i++] = priorityQueue.poll();
    }
}

排序总结

面试题：在Arrays的sort方法中，面对基础类型的默认使用快排，面对用户自定义的类型默认选择归并，这是为什么？

基于稳定性的考虑，基础类型的话稳定性不重要，而用户自定义的系统不知道需不需要稳定性，索性直接用稳定的归并排序算法。

4.链表

哈希表和有序表

Hash表简单介绍：

1. 有无伴随数据，是HashMap和HashSet唯一的区别，底层的实际结构是一回事
2. 使用哈希表增(put)、删(remove)、改(put)和查(get)的操作，可以认为时间复杂度为O(1)，但是常数时间比较大
3. 放入哈希表的东西，如果是基础类型，内部按值传递，内存占用就是这个东西的大小
4. 放入哈希表的东西，如果不是基础类型，内部按引用传递，内存占用是这个东西内存地址的大小

有序表简单介绍：

1. 有无伴随数据，是TreeSet和TreeMap唯一的区别，底层的实际结构是一回事

2. 有序表和哈希表的区别是，有序表把key按照顺序组织起来，而哈希表完全不组织，时间复杂度也稍大一点是O(logN)

3. 红黑树、AVL树、size-balance-tree和跳表等都属于有序表结构，只是底层具体实现不同

4. 有序表固定操作：

   1）void put(K key,V value)：将一个（key，value）记录加入到表中，或者将key的记录更新成value。
   2）V get(K key)：根据给定的key，查询value并返回。
   3）void remove(K key)：移除key的记录。
   4）boolean containsKey(K key)：询问是否有关于key的记录。
   5）K firstKey()：返回所有键值的排序结果中，最左（最小）的那个。
   6）K lastKey()：返回所有键值的排序结果中，最右（最大）的那个。
   7）K floorKey(K key)：如果表中存入过key，返回key；否则返回所有键值的排序结果中，key的前一个。
   8）K ceilingKey(K key)：如果表中存入过key，返回key；否则返回所有键值的排序结果中，key的后一个。

   以上所有操作时间复杂度都是O(logN)，N为有序表含有的记录数

链表简单题

【题目】分别实现反转单向链表和反转双向链表的函数

【要求】如果链表长度为N，时间复杂度要求为O(N)，额外空间复杂度要求为O(1)

//反转单向
public static Node reverseList(Node head){
    Node pre = null;
    Node next = null;
    while (head!=null){
        next = head.next;
        head.next = pre;
        pre = head;
        head = next;
    }
    return pre;
}

//反转双向
public static DoubleNode reverseDoubleList(DoubleNode head){
    DoubleNode pre = null;
    DoubleNode next = null;
    while(head!=null){
        next = head.next;
        head.next = pre;
        head.last = next;
        pre = head;
        head = next;
    }
    return pre;
}

【题目】给定两个有序链表的头指针head1和head2，打印两个链表的公共部分。

【要求】如果两个链表的长度之和为N，时间复杂度要求为O(N)，额外空间复杂度要求为O(1)

public static void function(Node head1,Node head2){
    System.out.print("Common Part:");
    while (head1!=null&&head2!=null){
        if(head1.value<head2.value){
            head1 = head1.next;
        }else if(head1.value>head2.value){
            head2 = head2.next;
        }else {
            System.out.print(head1.value+" ");
            head1 = head1.next;
            head2 = head2.next;
        }
    }
}

判断回文结构

【题目】给定一个单链表的头节点head，请判断该链表是否为回文结构。

【例子】1->2->1，返回true；1->2->2->1，返回true；15->6->15，返回true；1->2->3，返回false。

【要求】如果链表长度为N，时间复杂度达到O(N)，额外空间复杂度达到O(1)。

先说不考虑空间复杂度为O(1)的情况，我们可以通过栈来方便的判断链表是否为回文结构。

//栈，需要额外空间，空间复杂度O(N)
public static boolean function1(Node head){
    Stack<Node> stack = new Stack<Node>();
    Node temp = head;
    while(temp!=null){
        stack.push(temp);
        temp = temp.next;
    }
    while (head != null) {
        Node pop = stack.pop();
        if(head.value!= pop.value){
            return false;
        }
        head = head.next;
    }
    return true;
}

//快慢指针，需要额外N/2空间
public static boolean function2(Node head){
    if (head == null || head.next == null) {
        return true;
    }
    Node n1 = head;
    Node n2 = head;
    while (n2.next != null && n2.next.next != null) {
        n1 = n1.next;   // n1 -> mid
        n2 = n2.next.next;  //n2 -> end
    }
    n1 = n1.next;//right part first
    Stack<Node> stack = new Stack<>();
    while (n1 != null) {
        stack.push(n1);
        n1 = n1.next;
    }
    while (!stack.isEmpty()){
        if(head.value!=stack.pop().value){
            return false;
        }
        head = head.next;
    }
    return true;
}

如果需要通过有限几个变量来实现判断，我们需要用快慢指针确定中点位置后将后面的链表反转，和左边的逐一比较，比较完后需要将反转的链表复原。

//need O(1) space
public static boolean function3(Node head){
    if (head == null || head.next == null) {
        return true;
    }
    Node n1 = head;
    Node n2 = head;
    while (n2.next != null && n2.next.next != null) {
        n1 = n1.next;   // n1 -> mid
        n2 = n2.next.next;  //n2 -> end
    }
    n2 = n1.next;//right part first
    Node n3 = null;
    while(n2!=null){//right part reverse
        n1 = n2.next;
        n2.next = n3;
        n3 = n2;
        n2 = n1;
    }
    boolean res = true;
    n1 = n3;//right part last
    n2 = head;
    while (n2!=null&&n3!=null){
        if(n2.value!=n3.value){
            res = false;
            break;
        }
        n2 = n2.next;
        n3 = n3.next;
    }
    //recover list
    n3 = null;
    while(n1!=null){
        n2 = n1.next;
        n1.next = n3;
        n3 = n1;
        n1 = n2;
    }
    return res;
}

链表荷兰国旗问题

【题目】
给定一个单链表的头节点head，节点的值类型是整型，再给定一个整数pivot。实现一个调整链表的函数，将链表调整为左部分都是值小于pivot的节点，中间部分都是值等于pivot的节点，右部分都是值大于pivot的节点。

解题思路：将链表复制到数组中，利用荷兰国旗问题思想解决，需要额外N空间

//方法一：将链表复制到数组中，利用荷兰国旗问题思想解决，需要额外N空间
public static Node function1(Node head,int pivot){
    if(head==null||head.next==null&&head.next.next==null){
        return head;
    }
    Node cur = head;
    int i = 0;
    while (cur!=null){
        i++;
        cur = cur.next;
    }
    Node[] arr = new Node[i];
    cur = head;
    //将链表复制到数组中
    for(i=0;i<arr.length;i++){
        arr[i] = cur;
        cur = cur.next;
    }
    arrPartition(arr,pivot);
    for (i=1;i<arr.length;i++){
        arr[i-1].next = arr[i];
    }
    arr[i-1].next = null;
    return arr[0];
}

/*荷兰国旗思想：分成小于右边界，大于左边界
    * 当前值小于划分值，当前值和<区域的后一个值交换，<区域右扩，i++
    * 当前值等于划分值，i++
    * 当前值大于划分值，当前值和>区域前一个值交换，>区域左扩，i不变
    * */
private static void arrPartition(Node[] arr, int pivot) {
    int left = -1;//左边界
    int right = arr.length;//右边界
    int i = 0;
    while(i!=right){
        if(arr[i].value<pivot){
            swap(arr,i++,++left);
        }else if (arr[i].value>pivot){
            swap(arr,i,--right);
        }else {
            i++;
        }
    }
}

public static void swap(Node[] nodeArr, int a, int b) {
    Node tmp = nodeArr[a];
    nodeArr[a] = nodeArr[b];
    nodeArr[b] = tmp;
}

【进阶】在实现原问题功能的基础上增加如下的要求
【要求】调整后所有小于pivot的节点之间的相对顺序和调整前一样
【要求】调整后所有等于pivot的节点之间的相对顺序和调整前一样
【要求】调整后所有大于pivot的节点之间的相对顺序和调整前一样
【要求】时间复杂度请达到O(N)，额外空间复杂度请达到O(1)。

解题思想：分为三个链表，依次插入，最后链接起来。

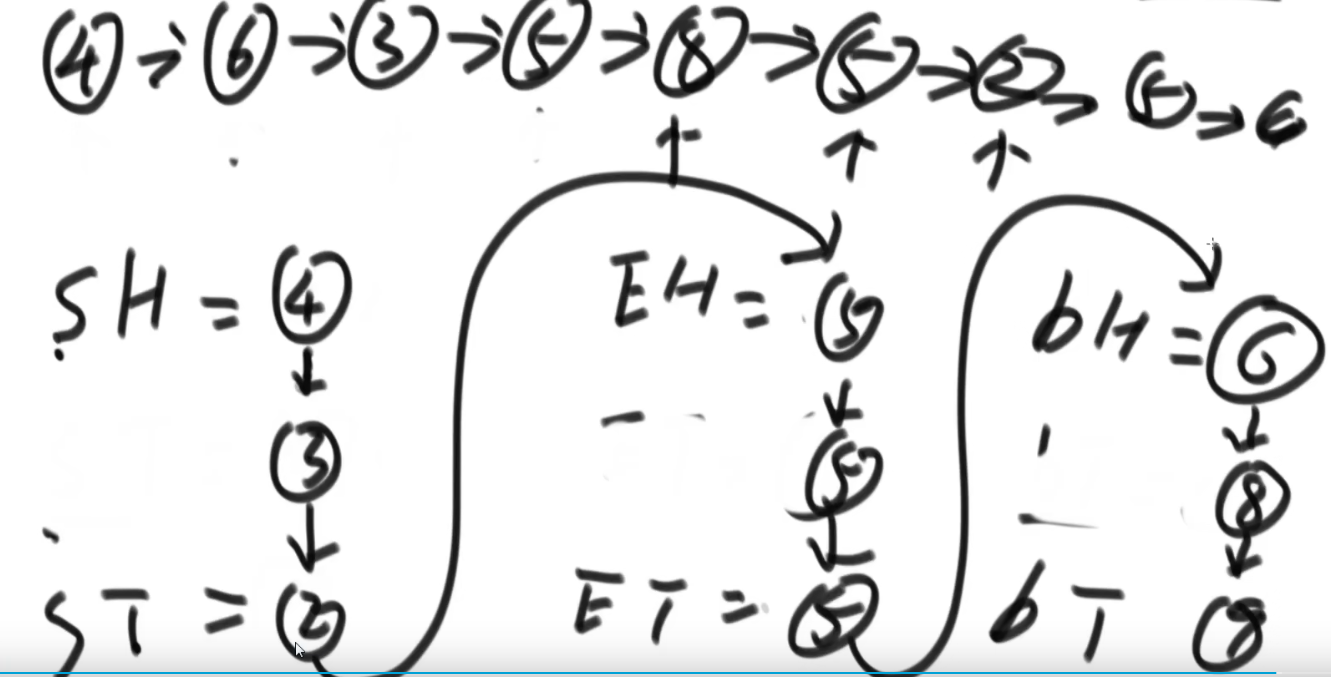
public static Node function2(Node head,int pivot){
    if(head==null||head.next==null&&head.next.next==null){
        return head;
    }
    Node sH = null; // small head
    Node sT = null; // small tail
    Node eH = null; // equal head
    Node eT = null; // equal tail
    Node bH = null; // big head
    Node bT = null; // big tail
    Node next = null;
    while(head!=null){
        next = head.next;
        head.next = null;
        if(head.value<pivot){
            if(sH==null){
                sH = head;
                sT = head;
            }else {
                sT.next = head;
                sT = head;
            }
        }else if(head.value==pivot){
            if(eH==null){
                eH = head;
                eT = head;
            }else {
                eT.next = head;
                eT = head;
            }
        }else {
            if(bH==null){
                bH = head;
                bT = head;
            }else {
                bT.next = head;
                bT = head;
            }
        }
        head = next;
    }
    //small and equal reconnect
    if(sH!=null){
        sT.next = eH;
        //谁去链接大于的头，谁就变成et
        eT = eT==null?sT:eT;
    }
    //all reconnect
    if(eT!=null){
        eT.next = bH;
    }
    return sH!=null?sH:eH!=null?eH:bH;
}

复制含有随机指针的链表

【题目】
一种特殊的单链表节点类描述如下

public class Node {
    public int value;
    public Node next;
    public Node rand;
    public Node(int value) {
        this.value = value;
    }
}

rand指针是单链表节点结构中新增的指针，rand可能指向链表中的任意一个节点，也可能指向null。给定一个由Node节点类型组成的无环单链表的头节点head，请实现一个函数完成这个链表的复制，并返回复制的新链表的头节点。
【要求】时间复杂度O(N)，额外空间复杂度O(1)

//方法一：通过map结构，key存储源节点，value存储复制节点，复制节点的指向都可以通过map结构得到
//需要额外N的空间
public static Node function1(Node head){
    if (head == null) {
        return null;
    }
    HashMap<Node,Node> map = new HashMap<>();
    Node cur = head;
    while(cur!=null){
        map.put(cur,new Node(cur.value));
        cur = cur.next;
    }
    cur = head;
    while(cur!=null){
        map.get(cur).next = map.get(cur.next);
        map.get(cur).rand = map.get(cur.rand);
        cur = cur.next;
    }
    return map.get(head);
}

//方法二：每个节点后面都插入复制的节点形成一个链表，这样复制节点的位置也很好确认，空间复杂度为O(1)
public static Node function2(Node head){
    if (head == null) {
        return null;
    }
    Node cur = head;
    Node next = null;
    //copy node and link to every node
    while(cur!=null){
        next = cur.next;
        cur.next = new Node(cur.value);
        cur.next.next = next;
        cur = next;
    }
    cur = head;
    Node copyNode = null;
    while (cur!=null){
        next = cur.next.next;
        copyNode = cur.next;
        copyNode.rand = cur.rand!=null?cur.rand.next:null;
        cur = next;
    }
    Node res = head.next;
    cur = head;
    // split
    while (cur!=null){
        next = cur.next.next;
        copyNode = cur.next;
        cur.next = next;
        copyNode.next = next!=null?next.next:null;
        cur = next;
    }
    return res;
}

两单链表相交的一系列问题

【题目】给定两个可能有环也可能无环的单链表，头节点head1和head2。请实现一个函数，如果两个链表相交，请返回相交的第一个节点。如果不相交，返回null

【要求】如果两个链表长度之和为N，时间复杂度请达到O(N)，额外空间复杂度请达到O(1)。

//找到链表第一个入环节点，如果没有返回null
/*方法：用快慢指针找到
    * 快指针一次走两步，慢指针一次走一步，如果快指针变为null，则一定没有环
    * 快慢指针一定会相遇，相遇时快指针回到头节点，慢指针不变，快慢指针每次都走一步
    * 最后相遇的节点即是第一个入环节点
    * */
public static Node getLoopNode(Node head){
    if (head == null || head.next == null || head.next.next == null) {
        return null;
    }
    Node slow = head.next;
    Node fast = head.next.next;
    while(slow!=fast){
        if(fast.next==null||fast.next==null){
            return null;//无环
        }
        slow = slow.next;
        fast = fast.next.next;
    }
    fast = head;
    while(slow!=fast){
        slow = slow.next;
        fast = fast.next;
    }
    return slow;
}

//如果两个链表都无环，返回第一个相交节点，没有返回null
/*如果两个无环链表有相交节点，一定是Y的形状
    * 也就是两个的最后一个节点一定是同一个的节点，可以通过此判断是否有相交*/
public static Node noLoop(Node head1,Node head2){
    if (head1 == null || head2 == null) {
        return null;
    }
    Node cur1 = head1;
    Node cur2 = head2;
    int n = 0;
    while(cur1.next!=null){
        n++;
        cur1 = cur1.next;
    }
    while(cur2.next!=null){
        n--;
        cur2 = cur2.next;
    }
    //此时cur1和cur2都来到最后一个节点
    if(cur1!=cur2){
        return null;
    }
    cur1 = n>0?head1:head2;//谁长谁的头变为cur1
    cur2 = cur1==head1?head2:head1;//谁短谁的头变为cur2
    n = Math.abs(n);
    //长的链表先移动相差距离n
    while(n!=0){
        n--;
        cur1=cur1.next;
    }
    //两者相遇的第一个节点就是第一个入环节点
    while(cur1!=cur2){
        cur1 = cur1.next;
        cur2 = cur2.next;
    }
    return cur1;
}

//两个有环链表，返回第一个入环节点，没有返回null
/*讨论：
    * （1）两个有环但并不相交：返回null
    * （2）两个有环且入环节点是一个：同无环的Y类型
    * （3）两个有环且在环内相交：返回loop1或者loop2*/
public static Node bothLoop(Node head1,Node loop1,Node head2,Node loop2){
    Node cur1 = null;
    Node cur2 = null;
    if(loop1==loop2){//情况（2）
        cur1 = head1;
        cur2 = head2;
        int n = 0;
        while (cur1!=loop1){
            n++;
            cur1 = cur1.next;
        }
        while (cur2!=loop2){
            n--;
            cur2 = cur2.next;
        }
        cur1 = n>0?head1:head2;
        cur2 = cur1==head1?head2:head1;
        n = Math.abs(n);
        while(n!=0){
            n--;
            cur1 = cur1.next;
        }
        while(cur1!=cur2){
            cur1 = cur1.next;
            cur2 = cur2.next;
        }
        return cur1;
    }else{//情况1或者3；判断方法：让loop1移动，如果和loop2相遇则是情况3
        cur1 = loop1.next;
        while(cur1!=loop1){
            if(cur1 == loop2){
                return loop2;
            }
            cur1 = cur1.next;
        }
        return null;
    }
}

public static Node getIntersectNode(Node head1,Node head2){
    if (head1 == null || head2 == null) {
        return null;
    }
    Node loop1 = getLoopNode(head1);
    Node loop2 = getLoopNode(head2);
    if(loop1==null&&loop2==null){
        return noLoop(head1,head2);
    }
    if(loop1!=null&&loop2!=null){
        return bothLoop(head1,loop1,head2,loop2);
    }
    //一个有环一个无环必不可能相交
    return null;
}

5.二叉树

递归实现二叉树遍历

首先我们举一个简单的例子介绍递归序

想遍历这个二叉树我们写一个简单的递归

public void function(Node head){
    if(head==null){
        return;
    }
    function(head.left);
    function(head.right);
}

递归序：1,2,4,4,4,2,5,5,5,1,3,6,6,6,3,7,7,7,3,1

再分别看看我们的先序遍历，中序遍历，后序遍历：

先序（头左右）：1，2，4，5，3，6，7

中序（左头右）：4，2，5，1，6，3，7

后序（左右头）：4，5，2，6，7，3，1

我们发现一个规律：先序遍历就是在递归序中的元素第一次出现顺序的时候输出，中序是第二次，后序是第三次

//递归先序遍历
public static void preOrderRecur(Node head){
    if(head==null){
        return;
    }
    System.out.print(head.value+" ");
    preOrderRecur(head.left);
    preOrderRecur(head.right);
}

//递归中序遍历
public static void inOrderRecur(Node head){
    if(head==null){
        return;
    }
    inOrderRecur(head.left);
    System.out.print(head.value+" ");
    inOrderRecur(head.right);
}

//递归后序遍历
public static void posOrderRecur(Node head) {
    if (head == null) {
        return;
    }
    posOrderRecur(head.left);
    posOrderRecur(head.right);
    System.out.print(head.value + " ");
}

非递归实现二叉树遍历

先序遍历：先把头节点放到栈里，接着固定流程

1. 每次从栈中弹出一个节点记为cur
2. 打印（处理cur）
3. 把cur的右节点先放入栈中，再把左节点放入栈中（如果有的话）
4. 循环往复

public static void preOrderUnRecur(Node head){
    if(head!=null){
        Stack<Node> stack = new Stack<>();
        stack.push(head);
        Node cur = null;
        while (!stack.isEmpty()){
            cur = stack.pop();
            System.out.println(cur.value+" ");
            if(cur.right!=null){
                stack.push(cur.right);
            }
            if(cur.left!=null){
                stack.push(cur.left);
            }
        }
    }
}

后序遍历：创建两个栈，一个普通栈，一个收集栈，先把头节点放到普通栈里

1. 每次从普通栈中弹出一个节点记为cur
2. 将cur放入收集栈中
3. 先左再右（如果有的话）
4. 循环往复

分析：这样子普通栈里面弹出的顺序是头右左，则收集栈里面弹出的顺序就是左右头，也就是后序遍历

public static void posOrderUnRecur(Node head){
    if(head!=null){
        Stack<Node> s1 = new Stack<>();
        Stack<Node> s2 = new Stack<>();
        s1.push(head);
        Node cur = null;
        while(!s1.isEmpty()){
            cur = s1.pop();
            s2.push(cur);
            if(cur.left!=null){
                s1.push(cur.left);
            }
            if(cur.right!=null){
                s1.push(cur.right);
            }
        }
        while(!s2.isEmpty()){
            System.out.print(s2.pop().value+" ");
        }
    }
}

中序遍历：

先整棵树的左边界进栈，依次弹出的过程中打印出来，接着对弹出节点的右子树作上述操作循环往复。

public static void inOrderUnRecur(Node head){
    if(head!=null){
        Stack<Node> stack = new Stack<>();
        while (!stack.isEmpty()||head!=null){
            if(head!=null){
                stack.push(head);
                head = head.left;
            }else{
                head = stack.pop();
                System.out.print(head.value+" ");
                head = head.right;
            }
        }
    }
}

求一棵二叉树的宽度

public static int getTreeMaxWidth(Node head){
    if(head==null){
        return 0;
    }
    //队列
    LinkedList<Node> queue =new LinkedList<>();
    queue.add(head);
    //map->key:节点，value：层数
    HashMap<Node,Integer> levelMap = new HashMap<>();
    levelMap.put(head,1);
    Node cur = null;
    int curLevel = 1;//当前层数
    int curNodes = 0;//当前层数的节点数量
    int max = Integer.MIN_VALUE;
    while (!queue.isEmpty()){
        cur = queue.pop();
        if(levelMap.get(cur)==curLevel){
            curNodes++;
        }else{
            max = Math.max(max,curNodes);
            curLevel++;
            curNodes = 1;
        }
        //深度遍历先左后右
        if(cur.left!=null){
            queue.add(cur.left);
            levelMap.put(cur.left,curLevel+1);
        }
        if(cur.right!=null){
            queue.add(cur.right);
            levelMap.put(cur.right,curLevel+1);
        }
    }
    //最后一层比较
    max = Math.max(max,curNodes);
    return max;
}

二叉树的相关概念及其实现判断

如何判断一颗二叉树是否是搜索二叉树？（搜索二叉树：每个子树的左节点都比头节点小，右节点都比头节点大）

将二叉树中序遍历，应该得到的是一个递增的数列。

public static int cur = Integer.MIN_VALUE;

public static boolean isBts(Node head){
    if(head==null){
        return true;
    }
    boolean leftIs = isBts(head.left);
    if(leftIs==false){
        return false;
    }
    if(head.value<=cur){
        return false;
    }else {
        cur = head.value;
    }
    return isBts(head.right);
}

如何判断一颗二叉树是完全二叉树？

（1）任意节点有右无左返回false

（2）在（1）不违规的条件下，如果宽度遍历遇到了第一个左右子树不全的节点，后续的节点都是叶节点

public static boolean isCbt(Node head){
    if(head==null){
        return true;
    }
    LinkedList<Node> queue = new LinkedList<>();
    queue.add(head);
    Node cur = null;
    Node l = null;
    Node r = null;
    //左右树节点不全的事件是否已经发生
    boolean isComplete = false;
    while (!queue.isEmpty()){
        cur = queue.pop();
        l = cur.left;
        r = cur.right;
        if(
            (l==null&&r!=null) ||//有右无左
            (isComplete&&(l!=null||r!=null))//子树节点不全后面的节点不是叶节点
        ){
            return false;
        }
        if(l!=null){
            queue.add(l);
        }
        if(r!=null){
            queue.add(r);
        }
        if(l==null||r==null){
            isComplete = true;
        }
    }
    return true;
}

如何判断一颗二叉树是否是满二叉树？

满二叉树满足条件：深度h和节点个数n关系——n=2^h-1

public static class ReturnType{
    public int hight;
    public int num;
    public ReturnType(int hight, int num) {
        this.hight = hight;
        this.num = num;
    }
}

public static ReturnType process(Node x){
    if(x==null){
        return new ReturnType(0,0);
    }
    ReturnType leftData = process(x.left);
    ReturnType rightData = process(x.right);
    int hight = Math.max(leftData.hight,rightData.hight)+1;
    int num = leftData.num+rightData.num+1;
    return new ReturnType(hight,num);
}

public static boolean isFbt(Node head){
    if(head==null){
        return true;
    }
    return process(head).num==1<<process(head).hight-1;
}

如何判断一颗二叉树是否是平衡二叉树？

平衡二叉树：任意节点的左右两个子树高度差不超过1

public static class ReturnType{
    public boolean isBanlanced;
    public int hight;
    public ReturnType(boolean isBanlanced, int hight) {
        this.isBanlanced = isBanlanced;
        this.hight = hight;
    }
}

public static ReturnType process(Node x){
    if(x==null){
        return new ReturnType(true,0);
    }
    ReturnType leftData = process(x.left);
    ReturnType rightData = process(x.right);
    int hight = Math.max(leftData.hight,rightData.hight)+1;
    boolean isBanlanced = leftData.isBanlanced&&rightData.isBanlanced&&
        (Math.abs(leftData.hight- rightData.hight)<=1);
    return new ReturnType(isBanlanced,hight);
}

public static boolean isBt(Node head){
    return process(head).isBanlanced;
}

最低公共祖先节点

给定两个二叉树的节点node1和node2，找到他们的最低公共祖先节点

//o1,o2属于以head开头的树，找到o1和o2最低公共祖先节点
public static Node function1(Node head,Node o1,Node o2){
    if (head == null || head == o1 || head == o2) {
        return head;
    }
    HashMap<Node,Node> fatherMap = new HashMap<>();
    fatherMap.put(head,head);
    process(fatherMap,head);
    HashSet<Node> set = new HashSet<>();
    Node cur = o1;
    //将o1往上窜，记录到set中
    while(cur != head){
        set.add(cur);
        cur = fatherMap.get(cur);
    }
    set.add(head);
    cur = o2;
    while(cur != head){
        if(set.contains(cur)){
            return cur;
        }
        cur = fatherMap.get(cur);
    }
    return head;
}

private static void process(HashMap<Node, Node> fatherMap, Node head) {
    if(head==null){
        return;
    }
    fatherMap.put(head.left,head);
    fatherMap.put(head.right,head);
    process(fatherMap,head.left);
    process(fatherMap,head.right);
}


public static Node function2(Node head,Node o1,Node o2){
    if (head == null || head == o1 || head == o2) {
        return head;
    }
    Node left = function2(head.left,o1,o2);
    Node right = function2(head.right,o1,o2);
    if(left!=null&&right!=null){
        return head;
    }
    return left!=null?left:right;
}

后继节点

后继节点：在二叉树的中序遍历的序列中，node的下一个节点叫作node的后继节点。

【题目】现在有一种新的二叉树节点类型如下:

public static class Node{
    public int value;
    public Node left;
    public Node right;
    public Node parent;

    public Node(int data) {
        this.value = data;
    }
}

该结构比普通二叉树节点结构多了一个指向父节点的parent指针。

假设有一棵Node类型的节点组成的二叉树，树中每个节点的parent指针都正确地指向自己的父节点，头节点的parent指向null。只给一个在二叉树中的某个节点node，请实现返回node的后继节点的函数。

方法：分有右子树和没有右子树两种情况

有右子树：后继节点是右子树最左边的节点
没有右子树：后继节点是向上遍历是某个父节点的左节点的那个父节点，一直找不到就是整个树最右边的节点，指向null

public static Node getSuccessorNode(Node node){
    if(node==null){
        return node;
    }
    if(node.right!=null){//有右子树
        return getLeftMost(node.right);
    }else{//没有右子树
        Node parent = node.parent;
        while(parent!=null&&parent.left!=node){
            node = parent;
            parent = node.parent;
        }
        return parent;
    }
}

private static Node getLeftMost(Node node) {
    while(node.left!=null){
        node = node.left;
    }
    return node;
}

二叉树的序列化和反序列化

序列化：内存里的一棵树如何变成字符串形式
反序列化：从字符串形式变成内存里的树

public static String serializeByPre(Node head){
    if(head==null){
        return "#_";
    }
    String res = head.value+"_";
    res += serializeByPre(head.left);
    res += serializeByPre(head.right);
    return res;
}

public static Node deserializeByPre(String str){
    String[] values = str.split("_");
    LinkedList<String> queue = new LinkedList<>();
    for (int i = 0; i < values.length; i++) {
        queue.add(values[i]);
    }
    return process(queue);
}

private static Node process(LinkedList<String> queue) {
    String value = queue.pop();
    if(value.equals("#")){
        return null;
    }
    Node head = new Node(Integer.valueOf(value));
    head.left = process(queue);
    head.right = process(queue);
    return null;
}

折纸问题

请把一段纸条竖着放在桌子上，然后从纸条的下边向上方对折1次，压出折痕后展开。

此时折痕是凹下去的，即折痕突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折2次，压出折痕后展开，此时有三条折痕，从上到下依次是下折痕、下折痕和上折痕。

给定一个输入参数N，代表纸条都从下边向上方连续对折N次。请从上到下打印所有折痕的方向。

例如:N=1时，打印:down N=2时，打印:down down up

分析：我们自己拿出一个纸条来折叠，发现一个规律，每个新折痕都是在上一个旧折痕上下形成的，通常是上面凹下面凸

可以看成一个二叉树，中序遍历后就是折痕的顺序

//i——当前层数 N——总共层数
public static void process(int i,int N,boolean down){
    if(i>N){
        return;
    }
    //中序遍历
    process(i+1,N,true);
    System.out.println(down?"down":"up");
    process(i+1,N,false);
}

public static void paperLoading(int n){
    process(1,n,true);
}

6.图

图的存储方式

图的存储方式有很多种，如邻接表、邻接矩阵等等，这里介绍一种算法中通用的图的表示结构。

Graph:

public class Graph {
    public HashMap<Integer,Node> nodes;
    public HashSet<Edge> edges;

    public Graph(){
        nodes = new HashMap<>();
        edges = new HashSet<>();
    }
}

Node:

public class Node {
    public int value;
    public int in;
    public int out;
    public ArrayList<Node> nexts;
    public ArrayList<Edge> edges;

    public Node(int value) {
        this.value = value;
        in = 0;
        out = 0;
        nexts = new ArrayList<>();
        edges = new ArrayList<>();
    }
}

Edge:

public class Edge {
    public int weight;
    public Node from;
    public Node to;

    public Edge(int weight, Node from, Node to) {
        this.weight = weight;
        this.from = from;
        this.to = to;
    }
}

我们做题时只要按照我们自己定义的图的方式把题做出来，再写一个适配器把题目中图的结构转化为自己定义的结构就可以了。

如：二维数组：n*3 每行第一个元素代表权重，第二个代表出节点，第三个代表入节点。将这个结构转化为我们的图结构。

public static Graph createGraph(Integer[][] matrix){
    Graph graph = new Graph();
    for (int i = 0; i < matrix.length; i++) {
        Integer weight = matrix[i][0];
        Integer from = matrix[i][1];
        Integer to = matrix[i][2];
        if(!graph.nodes.containsKey(from)){
            graph.nodes.put(from,new Node(from));
        }
        if(!graph.nodes.containsKey(to)){
            graph.nodes.put(to,new Node(to));
        }
        Node fromNode = graph.nodes.get(from);
        Node toNode = graph.nodes.get(to);
        Edge edge = new Edge(weight,fromNode,toNode);
        fromNode.nexts.add(toNode);
        fromNode.out++;
        toNode.in++;
        fromNode.edges.add(edge);
        graph.edges.add(edge);
    }
    return graph;
}

宽度优先遍历和深度优先遍历

宽度优先遍历：

1，利用队列实现
2，从源节点开始依次按照宽度进队列，然后弹出
3，每弹出一个点，把该节点所有没有进过队列的邻接点放入队列
4，直到队列变空

public static void bfs(Node node){
    LinkedList<Node> queue = new LinkedList<>();
    HashSet<Node> set = new HashSet<>();
    queue.add(node);
    set.add(node);
    while (!queue.isEmpty()){
        Node cur = queue.pop();
        System.out.println(cur.value);
        for(Node next:cur.nexts){
            if(!set.contains(next)){
                set.add(next);
                queue.add(next);
            }
        }
    }
}

深度优先遍历：

1，利用栈实现
2，从源节点开始把节点按照深度放入栈，然后弹出
3，每弹出一个点，把该节点下一个没有进过栈的邻接点放入栈
4，直到栈变空

public static void dfs(Node node){
    if(node==null){
        return;
    }
    Stack<Node> stack = new Stack<>();
    HashSet<Node> set = new HashSet<>();
    stack.push(node);
    set.add(node);
    System.out.println(node.value);
    while(!stack.isEmpty()){
        Node cur = stack.pop();
        for(Node next:cur.nexts){
            if (!set.contains(next)) {
                System.out.println(next.value);
                stack.add(cur);
                stack.add(next);
                set.add(next);
                break;
            }
        }
    }
}

拓扑排序算法

适用范围：要求有向图，且有入度为0的节点，且没有环

//方法：找出入度为0的节点返回，并将他的影响消除，循环往复
public static List<Node> sortedTopology(Graph graph){
    //key-->某一个node  value-->剩余的入度
    HashMap<Node,Integer> inMap = new HashMap<>();
    //入度为0的节点才能进这个队列
    LinkedList<Node> zeroQueue = new LinkedList<>();
    for(Node node:graph.nodes.values()){
        inMap.put(node, node.in);
        if(node.in==0){
            zeroQueue.add(node);
        }
    }
    List<Node> res = new ArrayList<>();
    while(!zeroQueue.isEmpty()){
        Node cur = zeroQueue.pop();
        res.add(cur);
        for(Node node:cur.nexts){
            inMap.put(node,inMap.get(node)-1);
            if(inMap.get(node)==0){
                zeroQueue.add(node);
            }
        }
    }
    return res;
}

kruskal算法

适用范围：要求无向图

思想：将边按照从小到大顺序排好，按照顺序依次加边进图，每次都判断是否构成环

判断成环方法：把每个节点想象成一个单独的集合，每次边加进去符合要求的话将集合合并，如果加入边的入和出节点在一个集合中，则构成环。

public static class MySets{
    public HashMap<Node, List<Node>> setMap;

    public MySets(Collection<Node> nodes){
        for(Node cur:nodes){
            List<Node> set = new ArrayList<>();
            set.add(cur);
            setMap.put(cur,set);
        }
    }

    public boolean isSameSet(Node from,Node to){
        List<Node> fromSet = setMap.get(from);
        List<Node> toSet = setMap.get(to);
        return fromSet==toSet;
    }

    public void union(Node from,Node to){
        List<Node> fromSet = setMap.get(from);
        List<Node> toSet = setMap.get(to);
        for(Node cur:toSet){
            fromSet.add(cur);
            setMap.put(cur,fromSet);
        }
    }
}

public static class EdgeComparator implements Comparator<Edge>{

    @Override
    public int compare(Edge o1, Edge o2) {
        return o1.weight- o2.weight;
    }
}


public static Set<Edge> kruskal(Graph graph){
    MySets mySets = new MySets(graph.nodes.values());
    PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
    //将边按顺序放入队列
    for(Edge edge:graph.edges){
        priorityQueue.add(edge);
    }
    Set<Edge> res = new HashSet<>();
    while(!priorityQueue.isEmpty()){
        Edge edge = priorityQueue.poll();
        if(!mySets.isSameSet(edge.from,edge.to)){//不是一个集合内的
            res.add(edge);
            mySets.union(edge.from,edge.to);
        }
    }
    return res;
}

Prim算法

思想：任意找一个点存入集合，选中它的边中权重最小的一条对应的节点存入集合中，接着循环往复。如果选中的边对应的节点已放入集合中，则跳过。

public static class EdgeComparator implements Comparator<Edge> {

    @Override
    public int compare(Edge o1, Edge o2) {
        return o1.weight- o2.weight;
    }
}

public static Set<Edge> prim(Graph graph){
    PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
    HashSet<Node> set = new HashSet<>();
    Set<Edge> res = new HashSet<>();
    for(Node node:graph.nodes.values()){//任意找一个点
        if(!set.contains(node)){
            set.add(node);
            for(Edge edge:node.edges){
                priorityQueue.add(edge);
            }
            while (!priorityQueue.isEmpty()){
                Edge edge = priorityQueue.poll();
                Node toNode = edge.to;
                if(!set.contains(toNode)){
                    set.add(toNode);
                    res.add(edge);
                    for(Edge nextEdge:toNode.edges){
                        priorityQueue.add(nextEdge);
                    }
                }
            }
        }
    }
    return res;
}

Dijkstra算法

适用范围：没有权值相和为负数的环

Dijkstra是求图上某个点到其他点的最短距离

public static HashMap<Node,Integer> dijkstra(Node head){
    //从head出发到所有点的最短距离
    //key——>点   value——>最短距离
    //如果没有记录，默认距离是正无穷
    HashMap<Node,Integer> distanceMap = new HashMap<>();
    distanceMap.put(head,0);
    //已经求过距离的节点放入selectedNode再也不碰
    HashSet<Node> selectedNode = new HashSet<>();
    Node minNode = getMinDistanceAndUnselectedNode(distanceMap,selectedNode);
    while (minNode!=null){
        int distance = distanceMap.get(minNode);
        for(Edge edge:minNode.edges){
            Node toNode = edge.to;
            if(!distanceMap.containsKey(toNode)){
                distanceMap.put(toNode,distance+edge.weight);
            }
            distanceMap.put(edge.to,Math.min(distanceMap.get(toNode),distance+edge.weight));
        }
        selectedNode.add(minNode);
        minNode = getMinDistanceAndUnselectedNode(distanceMap,selectedNode);
    }
    return distanceMap;
}

private static Node getMinDistanceAndUnselectedNode(HashMap<Node, Integer> distanceMap, HashSet<Node> selectedNode) {
    Node minNode = null;
    int minDistance = Integer.MAX_VALUE;
    for(Map.Entry<Node,Integer> entry:distanceMap.entrySet()){
        Node node = entry.getKey();
        int distance = entry.getValue();
        if(!selectedNode.contains(node)&&distance<minDistance){
            minNode = node;
            minDistance = distance;
        }
    }
    return minNode;
}

7.前缀树和贪心算法

前缀树

Trie树，即字典树，又称单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。

Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
它有3个基本性质：

1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。

好比假设有b，abc，abd，bcd，abcd，efg，hii 这6个单词，我们构建的树就是如下图这样的：

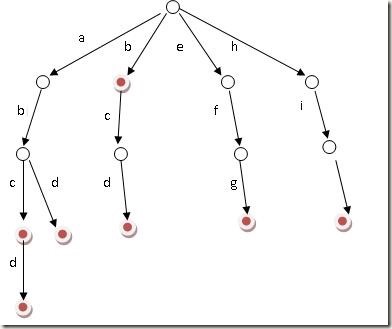
public static class TrieNode{
    public int pass;//经过次数
    public int end;//该点是几个单词的结尾
    public TrieNode[] nexts;
    public TrieNode(){
        pass = 0;
        end = 0;
        nexts = new TrieNode[26];
    }
}

public static class Trie{
    private TrieNode root;

    public Trie(){
        root = new TrieNode();
    }

    public void insert(String word){
        if(word==null){
            return;
        }
        char[] chars = word.toCharArray();
        TrieNode node = root;
        int index = 0;
        for (int i = 0; i < chars.length; i++) {
            index = chars[i] - 'a';
            if(node.nexts[index]==null){
                node.nexts[index] = new TrieNode();
            }
            node = node.nexts[index];
            node.pass++;
        }
        node.end++;
    }

    //这个单词加入过几次
    public int search(String word){
        if(word==null){
            return 0;
        }
        char[] chars = word.toCharArray();
        TrieNode node = root;
        int index = 0;
        for (int i = 0; i < chars.length; i++) {
            index = chars[i] - 'a';
            if(node.nexts[index]==null){
                return 0;
            }
            node = node.nexts[index];
        }
        return node.end;
    }

    public void delete(String word){
        //先判断前缀树是否能查到此单词，查到才能删除
        if(search(word)!=0){
            char[] chars = word.toCharArray();
            TrieNode node = root;
            int index = 0;
            for (int i = 0; i < chars.length; i++) {
                index = chars[i] - 'a';
                if(--node.nexts[index].pass==0){
                    node.nexts[index] = null;
                    return;
                }
                node = node.nexts[index];
            }
            node.end--;
        }
    }

    //加入的字符串中有几个是pre作为前缀的
    public int prefixNumber(String pre){
        if (pre == null) {
            return 0;
        }
        char[] chs = pre.toCharArray();
        TrieNode node = root;
        int index = 0;
        for (int i = 0; i < chs.length; i++) {
            index = chs[i] - 'a';
            if (node.nexts[index] == null) {
                return 0;
            }
            node = node.nexts[index];
        }
        return node.pass;
    }
}

贪心算法

一些项目要占用一个会议室宣讲，会议室不能同时容纳两个项目的宣讲。给你每一个项目开始的时间和结束的时间(给你一个数组，里面是一个个具体的项目)，你来安排宣讲的日程，要求会议室进行的宣讲的场次最多。返回这个最多的宣讲场次。

public static class Program{
    public int start;
    public int end;

    public Program(int start, int end) {
        this.start = start;
        this.end = end;
    }
}

public static class ProgramComparator implements Comparator<Program>{

    @Override
    public int compare(Program o1, Program o2) {
        return o1.end- o2.end;
    }
}

//贪心策略：选结束时间最早的
public static int bestArrange(Program[] programs,int startTime){
    Arrays.sort(programs,new ProgramComparator());
    int result = 0;
    for (int i = 0; i < programs.length; i++) {
        if(startTime<=programs[i].start){
            result++;
            startTime = programs[i].end;
        }
    }
    return result;
}

一块金条切成两半，是需要花费和长度数值一样的铜板的。比如长度为20的金条，不管切成长度多大的两半，都要花费20个铜板。

一群人想整分整块金条，怎么分最省铜板?

例如,给定数组{10,20,30}，代表一共三个人，整块金条长度为10+20+30=60。金条要分成10,20,30三个部分。如果先把长度60的金条分成10和50，花费60；再把长度50的金条分成20和30，花费50；一共花费110铜板。但是如果先把长度60的金条分成30和30，花费60；再把长度30金条分成10和20，花费30；一共花费90铜板。输入一个数组，返回分割的最小代价。

很显然，我们用贪心策略就是先分大的，然后再分，反过来也就是从小的开始加，类似于Huffuman编码向上加到最大形成最短

public static int lessMoney(int[] arr){
    //PriorityQueue默认是小顶堆
    PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
    for(int a:arr){
        priorityQueue.add(a);
    }
    int sum = 0;
    int cur = 0;
    while (priorityQueue.size()>1){
        cur = priorityQueue.poll() + priorityQueue.poll();
        sum += cur;
        priorityQueue.add(cur);
    }
    return sum;
}

costs[i]表示i号项目的花费
profits[i]表示i号项目在扣除花费之后还能挣到的钱(利润)
k表示你只能串行的最多做k个项目
m表示你初始的资金

说明：你每做完一个项目，马上获得的收益，可以支持你去做下一个项目。
输出：你最后获得的最大钱数。

public static class Node{
    public int cost;
    public int profit;

    public Node(int cost, int progit) {
        this.cost = cost;
        this.profit = progit;
    }
}

public static class MinCostComprartor implements Comparator<Node>{

    @Override
    public int compare(Node o1, Node o2) {
        return o1.cost-o2.cost;
    }
}

public static class MaxProfitComparator implements Comparator<Node>{

    @Override
    public int compare(Node o1, Node o2) {
        return o2.profit- o1.profit;
    }
}

public static int findMaxMakeMoney(int k,int m,int[] costs,int[] profits){
    Node[] nodes = new Node[profits.length];
    for (int i = 0; i < profits.length; i++) {
        nodes[i] = new Node(costs[i],profits[i]);
    }
    PriorityQueue<Node> minCostQueue = new PriorityQueue<>(new MinCostComprartor());
    PriorityQueue<Node> maxProfitQueue = new PriorityQueue<>(new MaxProfitComparator());
    for (int i = 0; i < nodes.length; i++) {
        minCostQueue.add(nodes[i]);
    }
    for (int i = 0; i < k; i++) {
        /*peek和poll的区别
            * peek弹出但不删除，poll弹出并且从堆里删除*/
        while (!minCostQueue.isEmpty()&&minCostQueue.peek().cost<=m){
            maxProfitQueue.add(minCostQueue.poll());
        }
        while (maxProfitQueue.isEmpty()){
            return m;
        }
        m += maxProfitQueue.poll().profit;
    }
    return m;
}

一个数据流中，随时可以取得中位数

解题方法：创建一个大根堆一个小根堆，默认第一个元素放入大根堆，接下来元素做如下步骤：
（1）判断cur<=大堆顶，如果是，放入大根堆，不是放入小根堆
（2）大根堆和小根堆的size差距等于2的时候，让size较大的堆顶弹出元素放入size较小的堆

public static class MaxheapComparator implements Comparator<Integer>{

    @Override
    public int compare(Integer o1, Integer o2) {
        return o2-o1;
    }
}

public PriorityQueue<Integer> minHeap = new PriorityQueue<>();
public PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new MaxheapComparator());

public void modifySize(){
    if(maxHeap.size()==minHeap.size()+2){
        minHeap.add(maxHeap.poll());
    }
    if(minHeap.size()==maxHeap.size()+2){
        maxHeap.add(minHeap.poll());
    }
}

public void addNum(int num){
    if(maxHeap.isEmpty()||num<=maxHeap.peek()){
        maxHeap.add(num);
    }else {
        minHeap.add(num);
    }
    modifySize();
}

public int getMedian(int[] arrs){
    for(int arr:arrs){
        addNum(arr);
    }
    int minSize = minHeap.size();
    int maxSize = maxHeap.size();
    Integer minHeapHead = minHeap.peek();
    Integer maxHeapHead = maxHeap.peek();
    if((minSize+maxSize)%2==0){
        return (maxHeapHead+minHeapHead)/2;
    }else {
        return maxSize>minSize?maxHeapHead:minHeapHead;
    }
}

8.暴力递归

N皇后问题

皇后问题是指在N*N的棋盘上要摆N个皇后，要求任何两个皇后不同行、不同列，也不在同一条斜线上。给定一个整数n，返回n皇后的摆法有多少种。

n=1，返回1。n=2或3，2皇后和3皇后问题无论怎么摆都不行，返回0。n=8，返回92。

public static int num1(int n){
    if(n<1){
        return 0;
    }
    int[] record = new int[n];//record[i]->i行的皇后放在哪一列
    return process1(0,record,n);
}

/*
    * i:现在来到了第i行
    * record[0~i-1]表示之前放皇后的位置，record[0~i-1]的任意两个皇后一定不同行，不同列，不同斜线
    * n:总共多少行*/
public static int process1(int i,int[] record,int n){
    if(i==n){//终止行
        return 1;
    }
    int res = 0;
    //遍历i行的列，找到能放皇后的点
    for(int j=0;j<n;j++){
        if(isValid(record,i,j)){
            record[i] = j;
            res += process1(i+1,record,n);
        }
    }
    return res;
}

//需要符合record[0~i-1]才能放
private static boolean isValid(int[] record, int i, int j) {
    for (int k = 0; k < i; k++) {
        if(record[k]==j||Math.abs(k-i)==Math.abs(record[k]-j)){
            return false;
        }
    }
    return true;
}

利用位运算优化：N皇后问题时间复杂度永远是O(N!)，但是我们可以通过位运算来简便常数时间。

public static int num2(int n){
    if(n<1||n>32){//大于32位运算支持不了
        return 0;
    }
    int upperLim = n==32?-1:(1<<n)-1;//按位自右向左有n个1，其余为0
    return process2(upperLim,0,0,0);
}

//colLim-->列的限制，1的位置不能放皇后，0的位置可以放皇后
//leftLim->左斜线的限制，1的位置不能放皇后，0的位置可以放皇后
//rightLim-->右斜线的限制，1的位置不能放皇后，0的位置可以放皇后
public static int process2(int upperLim,int colLim,int leftLim,int rightLim){
    if(colLim==upperLim){//列已经放满了
        return 1;
    }
    //pos上1表示能放皇后
    int pos = upperLim & (~(colLim|leftLim|rightLim));
    int mostRightOne = 0;
    int res = 0;
    while(pos!=0){
        mostRightOne = pos & (~pos+1);//取出最右边的1
        pos = pos - mostRightOne;
        res += process2(upperLim,
                        colLim|mostRightOne,
                        (leftLim|mostRightOne)<<1,
                        (rightLim|mostRightOne)>>>1);// '>>>'表示无符号右移
    }
    return res;
}

编写一个测试类看看位运算对常数级别优化了多少

public static void main(String[] args) {
    int n = 14;

    long start = System.currentTimeMillis();
    System.out.println(num2(n));
    long end = System.currentTimeMillis();
    System.out.println("cost time: " + (end - start) + "ms");

    start = System.currentTimeMillis();
    System.out.println(num1(n));
    end = System.currentTimeMillis();
    System.out.println("cost time: " + (end - start) + "ms");

}

暴力递归解释

暴力递归就是尝试

1，把问题转化为规模缩小了的同类问题的子问题

2，有明确的不需要继续进行递归的条件(basecase)

3，有当得到了子问题的结果之后的决策过程

4，不记录每一个子问题的解

汉诺塔问题

打印n层汉诺塔从最左边移动到最右边的全部过程

public static void process(int i,String from,String to,String other){
    if(i==1){//base case
        System.out.println("move 1 from "+from+"to "+to);
    }else {
        //将1~i-1从from移动到other
        process(i-1,from,other,to);
        //将i从from移动到to
        System.out.println("move "+i+" from "+from+" to "+to);
        //将1~i-1从other移动到to
        process(i-1,other,to,from);
    }
}

public static void hanoi(int n){
    if(n>0){
        process(n,"左","右","中");
    }
}

字符串相关问题

打印一个字符串的全部子序列，包括空字符串

public static void printAllSubsquences(String str){
    char[] chs = str.toCharArray();
    process(chs,0);
}

//当前来到i位置，要或者不要该字符
public static void process(char[] chs,int i){
    if(i==chs.length){
        System.out.println(String.valueOf(chs));
        return;
    }
    char temp = chs[i];
    process(chs,i+1);//要当前字符的路
    chs[i] = 0;
    process(chs,i+1);//不要当前字符的路
    chs[i] = temp;//字符原封不动
}

打印一个字符串的全部排列，要求不要出现重复的排列

public static ArrayList<String> printAllPermutation(String str){
    char[] chs = str.toCharArray();
    ArrayList<String> res = new ArrayList<>();
    process(chs,0,res);
    return res;
}

//chs[0~i-1]表示已经确定好的排列
//i表示当前开始排列的位置
public static void process(char[] chs, int i, ArrayList<String> res){
    if(i==chs.length){
        res.add(chs.toString());
    }
    //不出现重复的排列
    boolean[] visit = new boolean[26];//默认初始化是flase
    for(int j=i;j<chs.length;j++){
        if(!visit[chs[j]-'a']){
            visit[chs[j]-'a'] = true;
            swap(chs,i,j);
            process(chs,i,res);
            swap(chs,j,i);
        }
    }
}

private static void swap(char[] chs, int i, int j) {
    char temp = chs[i];
    chs[i] = chs[j];
    chs[j] = temp;
}

纸牌游戏

给定一个整型数组arr，代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸牌，规定玩家A先拿，玩家B后拿，但是每个玩家每次只能拿走最左或最右的纸牌，玩家A和玩家B都绝顶聪明。请返回最后获胜者的分数。

【举例】
arr=[1,2,100,4]。开始时，玩家A只能拿走1或4。如果开始时玩家A拿走1，则排列变为[2,100,4]，接下来玩家B可以拿走2或4，然后继续轮到玩家A…如果开始时玩家A拿走4，则排列变为[1,2,100]，接下来玩家B可以拿走1或100，然后继续轮到玩家A…玩家A作为绝顶聪明的人不会先拿4，因为拿4之后，玩家B将拿走100。所以玩家A会先拿1，让排列变为[2,100,4]，接下来玩家B不管怎么选，100都会被玩家A拿走。玩家A会获胜，分数为101。所以返回101。
arr=[1,100,2]。开始时，玩家A不管拿1还是2，玩家B作为绝顶聪明的人，都会把100拿走。玩家B会获胜，分数为100。所以返回100。

public static int win(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    return Math.max(f(arr, 0, arr.length - 1), s(arr, 0, arr.length - 1));
}

//先手
public static int f(int[] arr,int L,int R){
    if(L==R){
        return arr[L];
    }
    return Math.max(arr[L]+s(arr,L+1,R),arr[R]+s(arr,L,R-1));
}

//后手
private static int s(int[] arr, int L, int R) {
    if(L==R){
        return 0;
    }
    return Math.min(f(arr,L+1,R),f(arr,L,R-1));
}

逆序栈

给你一个栈，请你逆序这个栈，不能申请额外的数据结构，只能使用递归函数。

public static void reverseStack(Stack<Integer> stack){
    if(stack.isEmpty()){
        return;
    }
    int i = getAndRemoveLastElement(stack);
    reverseStack(stack);
    stack.push(i);
}

public static int getAndRemoveLastElement(Stack<Integer> stack){
    int result = stack.pop();
    if(stack.isEmpty()){
        return result;
    }else {
        int last = getAndRemoveLastElement(stack);
        stack.push(result);
        return last;
    }
}

字母转化

规定1和A对应、2和B对应、3和C对应…那么一个数字字符串比如”111”，就可以转化为”AAA”、”KA”和”AK”。

给定一个只有数字字符组成的字符串str，返回有多少种转化结果。

public static int number(String str) {
    if (str == null || str.length() == 0) {
        return 0;
    }
    return process(str.toCharArray(), 0);
}

//chs[0~i-1]已确定转化,从i开始判断转化成什么
//返回转化的种类个数
public static int process(char[] chs,int i){
    if(i==chs.length){
        return 1;
    }
    if(chs[i]=='0'){
        return 0;
    }
    if(chs[i]=='1'){
        int res = process(chs,i+1);//i自己作为单独的部分，后面有多少种方法
        if(i+1<chs.length){
            res += process(chs,i+2);// i和(i+1)作为单独部分
        }
        return res;
    }
    if(chs[i]=='2'){
        int res = process(chs,i+1);//i自己作为单独的部分，后面有多少种方法
        if(i+1<chs.length && chs[i+1]>='0' &&chs[i+1]<='6'){
            res += process(chs,i+2);
        }
    }
    //3-6没有后续部分能结合
    return process(chs,i+1);
}

背包问题

给定两个长度都为N的数组weights和values，weights[i]和values[i]分别代表i号物品的重量和价值。给定一个正数bag，表示一个载重bag的袋子，你装的物品不能超过这个重量。返回你能装下最多的价值是多少？

public static int maxValue(int[] weight,int[] value,int bag){
    return process(weight,value,0,0,bag);
}

public static int process(int[] weight,int[] values,int i,int alreadyWeight,int bag){
    if(alreadyWeight>bag){
        return 0;
    }
    if(i==weight.length){
        return 0;
    }
    return Math.max(
        process(weight,values,i+1,alreadyWeight,bag),
        values[i]+process(weight,values,i+1,alreadyWeight+weight[i],bag)
    );
}

赏

谢谢你请我吃糖果

支付宝

微信