数学建模—线性规划与LINGO编程


阅读数: 次   

EverydayOneCat

06ddb948beb84220cf26905c392c70075d33a311

知识点

1.笔记

image-20200720110841677

2.数学规划

数学规划指在一系列客观或主观限制条件下，寻求合理分配有限资源，使所关注的某个或多个指标达到最大（或最小）的数学理论和方法

最优化数学模型的一般形式：

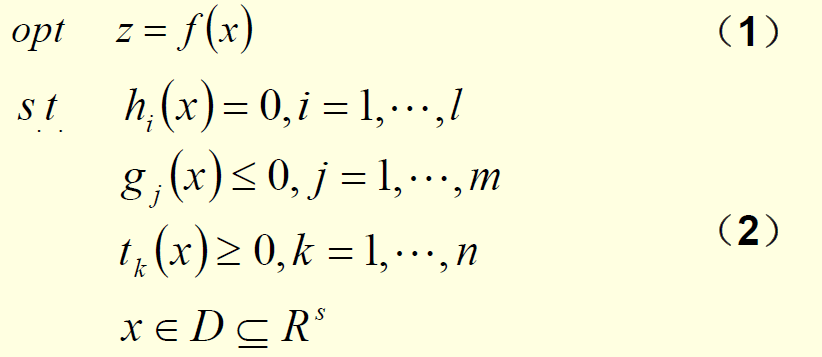
image-20200718150254500

三个要素：决策变量decision variable，目标函数objective function，约束条件constraints。

2.1运输问题(经典)

有两个粮库A1、A2向三个粮站B1、B2、B3调运大米，两个粮库现存大米分别4吨、8吨，三个粮站至少需要大米分别为2、4、5吨，两个粮库到三个粮站的距离（单位：公里）如下：问如何调运使运费最低。

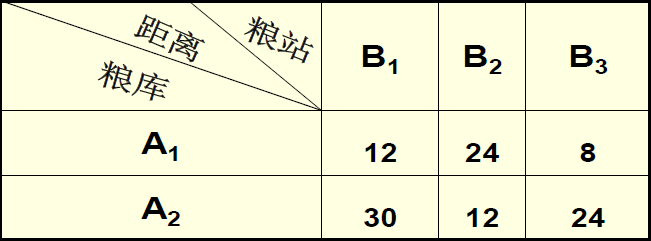
image-20200718150407330

设粮库A1、A2调运到三个粮站B1、B2 、B3的大米重量分别为x1，x2， x3， x4， x5， x6

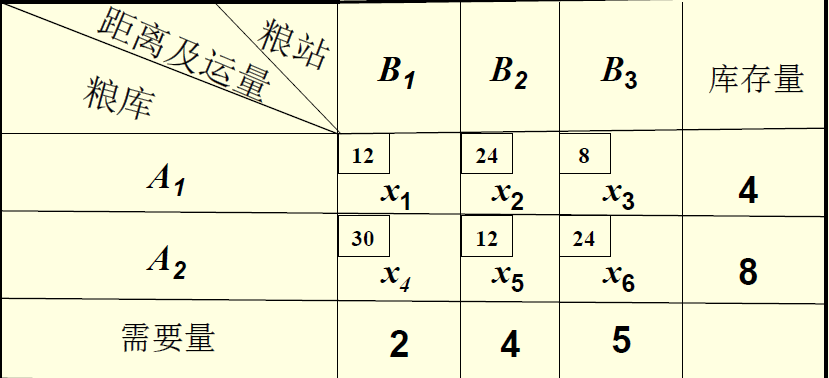
image-20200718150438986

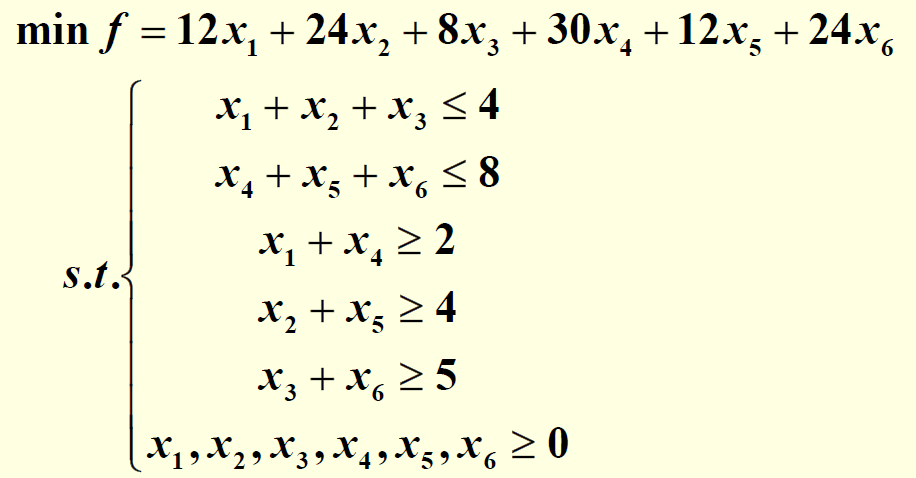
image-20200718150501443

LinGo代码：(LinGo默认变量都为非负数)

1
2
3
4
5
6
7
8
model:
min=12*x1+24*x2+8*x3+30*x4+12*x5+24*x6 ;
x1+x2+x3<4 ;
x4+x5+x6<8 ;
x1+x4>2 ;
x2+x5>4 ;
x3+x6>5 ;
end

运行结果：

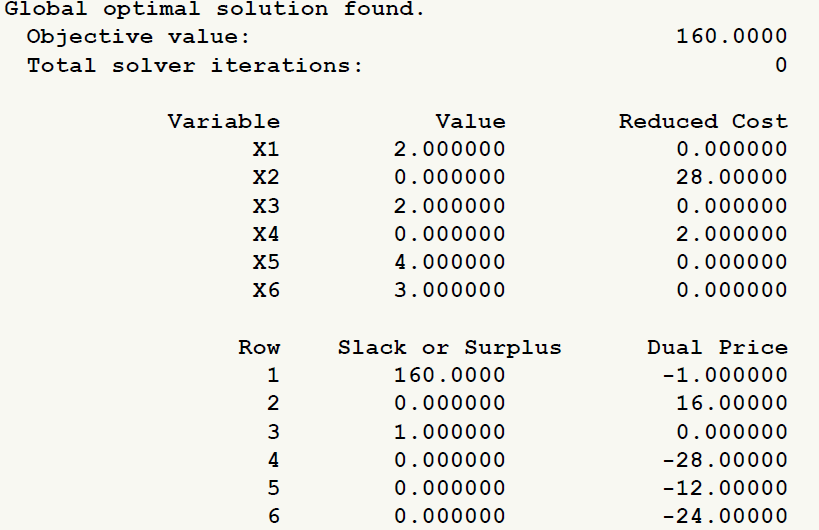
image-20200718150614411

我们在数学建模中有一套标准，变量更换为：

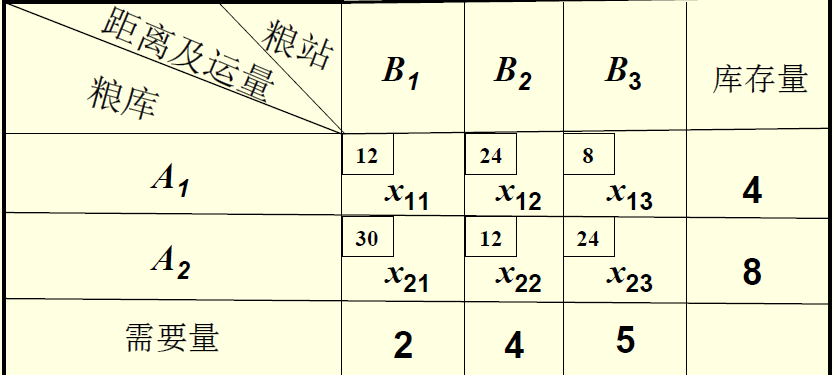
image-20200718150811365

建立数学模型：

image-20200718150835965

Lingo代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
model:
sets:
lk/1..2/:a;
lz/1..3/:b;
link(lk,lz):c,x;
endsets
data:
a=4,8;
b=2,4,5;
c=12,24,8,30,12,24;
enddata
min=@sum(link(i,j):c(i,j)*x(i,j));
@for(lk(i):@sum(lz(j):x(i,j))<a(i));
@for(lz(j):@sum(lk(i):x(i,j))>b(j));
end

image-20200718151104801

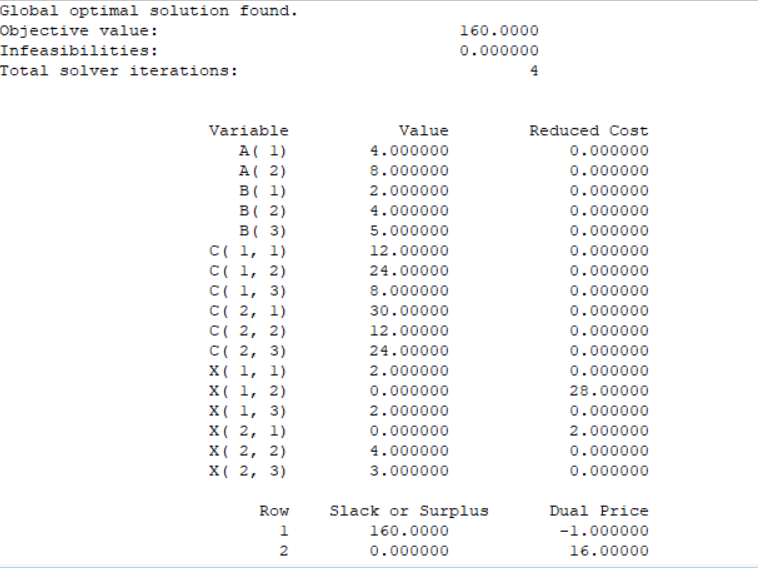
image-20200718151132890

2.2阶段生产问题(经典)

某公司生产某产品，最大生产能力为10000单位，每单位存储费2元，预定的销售量与单位成本如下:

image-20200718162333393

求生产计划：使1)满足需求; 2)不超过生产能力;3)成本(生产成本与存储费之和)最低.

解：假定1月初无库存，4月底卖完，当月生产的不库存，库存量无限制。

模型1：

image-20200718162540031

根据模型编写Lingo代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
model:
sets:
yue/1..4/:x,c,d;
endsets
data:
a=10000;
e=2;
c=70 71 80 76;
d=6000 7000 12000 6000;
enddata
min=@sum(yue:c*x)+@sum(yue(j)|j#le#3:@sum(yue(i)|i#le#j:x-d)*e);
@for(yue(j)|j#le#3:@sum(yue(i)|i#le#j:x)>@sum(yue(i)|i#le#j:d));
@sum(yue:x)=@sum(yue:d);
@for(yue:x<a);
end

这里需要注意：|#le#是小于等于；lt是小于，ge是大于等于，gt是大于，ne是不等于

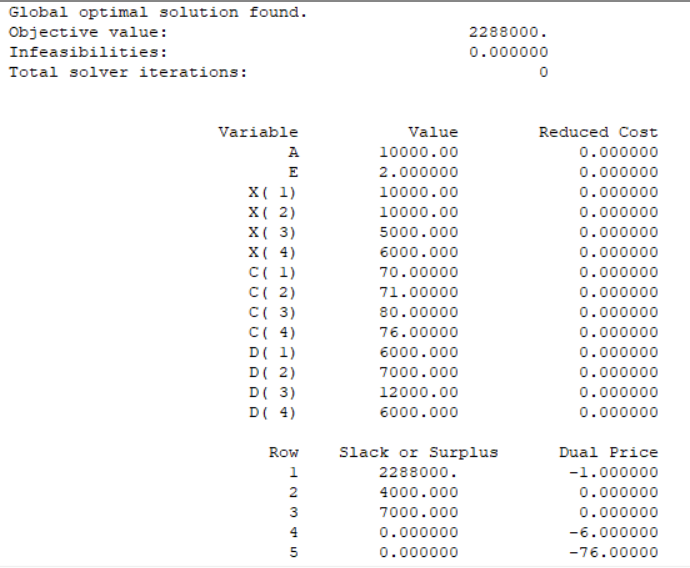
image-20200718162809948

模型2：

image-20200718173613307

根据模型编写Lingo代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
model:
sets:
yue/1..4/:x,c,d,s;
endsets
data:
a=10000;
e=2;
c=70 71 80 76;
d=6000 7000 12000 6000;
enddata
min=@sum(yue:c*x+s*e);
@for(yue(i)|i#le#3:s(i+1)=s(i)+x(i)-d(i));
s(1)=0;
s(4)+x(4)-d(4)=0;
@for(yue:x<a);
end

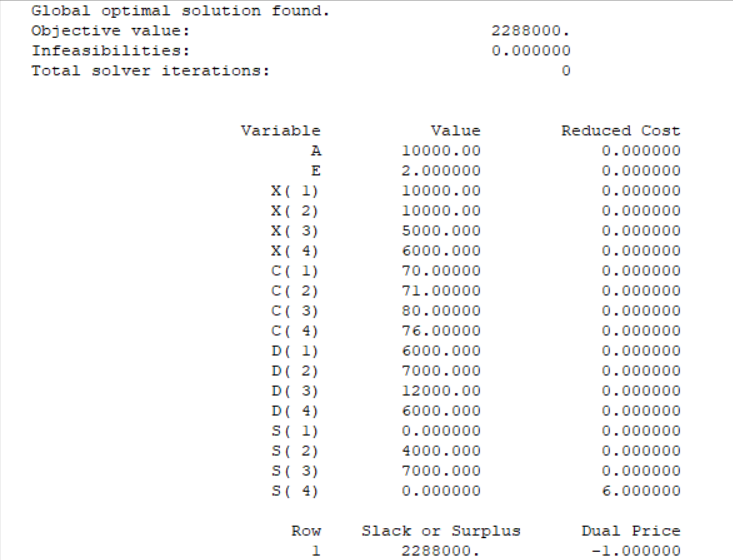
image-20200718180357531

2.3灵敏度分析

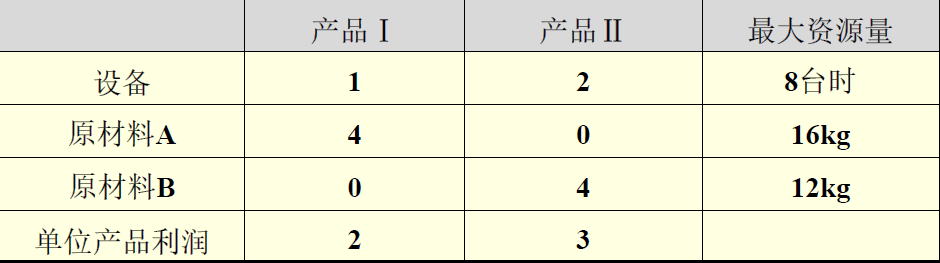
生产计划问题某工厂计划安排生产Ⅰ、Ⅱ两种产品，已知每种单位产品的利润，生产单位产品所需设备台时及A、B两种原材料的消耗，现有原材料和设备台时的定额如表所示，问：
１）怎么安排生产使得工厂获利最大？
２）产品Ⅰ的单位利润降低到1.8万元，改变生产计划吗？降低到1万元呢？
３）产品Ⅱ的单位利润增大到5万元，要不要改变生产计划？
４）如果产品Ⅰ、Ⅱ的单位利润同时降低了1万元，要不要改变生产计划？

image-20200719141609092

编写Lingo代码：

1
2
3
4
5
6
7
model:
title 生产计划问题;
max=2*x1+3*x2;
x1+2*x2<8;
4*x1<16;
4*x2<12;
END

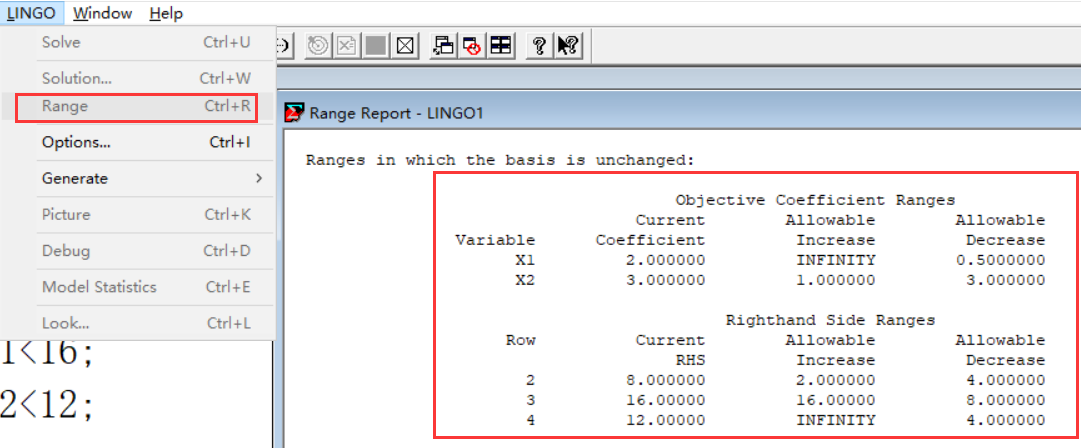
image-20200719141733926

我们可以看出，产品Ⅰ的单位利润降低到1.8万元，在（1.5，∞）之间，所以不改变生产计划；如果降低到1万元，不在（1.5，∞）
内，要改变生产计划。

产品Ⅱ的单位利润增大到5万元，要改变生产计划。

注意：敏感性分析只做改变一项的分析！所以如果产品Ⅰ、Ⅱ的单位利润同时降低了1万元，因为两个系数同时改变了，只有更改程序的数据，重新运行。

2.4加工奶制品的生产计划

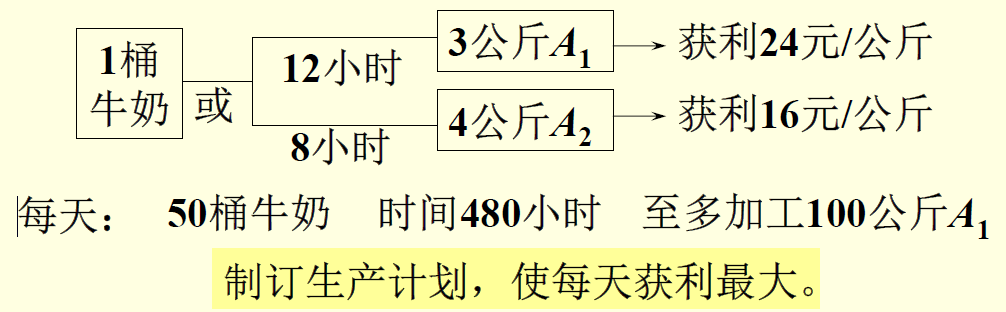
image-20200719144826131

1、35元可买到1桶牛奶，买吗？若买，每天最多买多少?
2、可聘用临时工人，付出的工资最多是每小时几元?
3、A1的获利增加到30元/公斤，改变生产计划吗？

这里我们需要考虑到建立初始模型时尽量不出现分式，方便后续的稳定性灵敏度分析

image-20200719144952591

1
2
3
4
5
6
Model:
max=72*x1+64*x2;
x1+x2<50;
12*x1+8*x2<480;
3*x1<100;
end

image-20200719145027063

影子价格的经济含义：在最优方案中，该资源每增加一个单位所带来的总收益的增加量。

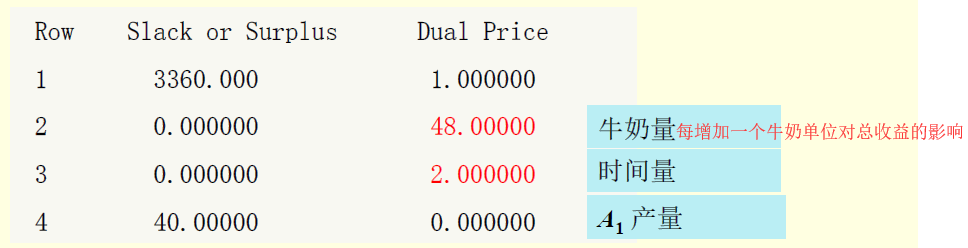
image-20200719145208437

1、35元可买到1桶牛奶，要买吗？ 答：35 <48， 应该买！

2、聘用临时工人付出的工资最多每小时几元？ 答：2元！

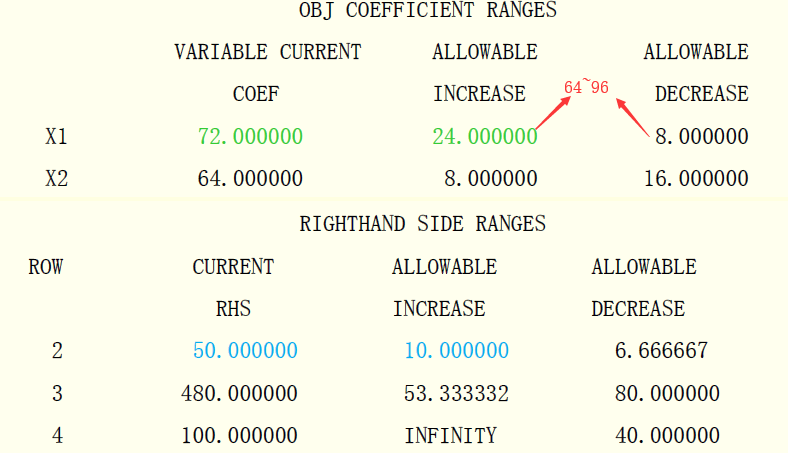
image-20200719145356810

3、A1获利增加到30元/千克，改变生产计划吗？ 答：30在(64~96)/3范围中，所以生产计划不变！
4、若35元买，每天最多买多少桶？ 答：最多买10桶！

3.整数规划与（0-1）规划

3.1下料问题(经典)

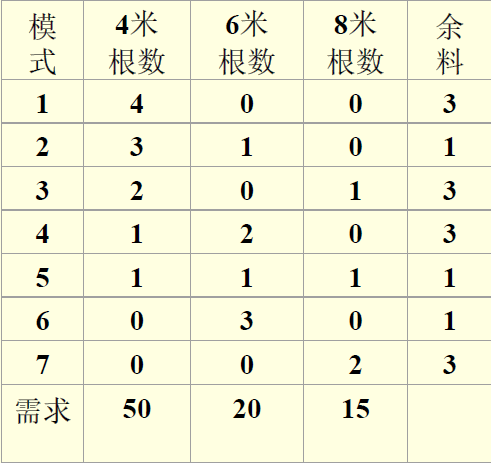
原料钢管：每根19米。客户需求：4米50根、6米20根、8米15根。问题： 如何下料最节省？

合理切割模式的余料应小于客户需要钢管的最小尺寸

模型一：

决策变量：xi ：按第i 种模式切割的原料钢管的根数(i=1,2,…7)

目标函数：

image-20200719165143157

image-20200719165215334

根据模型编写Lingo代码：(@gin整数约束)

1
2
3
4
5
6
7
8
model:
Title 钢管下料;
Min=x1 + x2 + x3 + x4 + x5 + x6 + x7;
4*x1 + 3*x2 + 2*x3 + x4 + x5>50;
x2 + 2*x4 + x5 + 3*x6> 20;
x3 + x5 + 2*x7>15;
@gin(x1);@gin(x2);@gin(x3);@gin(x4);@gin(x5);@gin(x6);@gin(x7);
end

模型二：更有推广性

设xi: 按第i种模式切割原料钢管的根数
cij: 一根钢管按第i种模式切割出第j种类型的根数
bj: 第j种类型的需要根数（i=1,…,7， j=1,2,3）

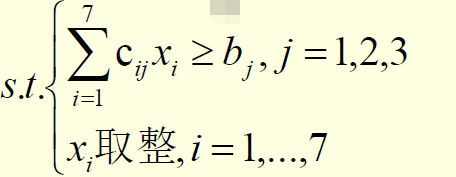
image-20200719170010543

根据模型编写Lingo代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
model:
sets:
ms/1..7/:x;
lx/1..3/:b;
link(ms,lx):c;
endsets
data:
b=50 20 15;
c= 4 0 0 3 1 0 2 0 1 1 2 0 1 1 1 0 3 0 0 0 2;
enddata
min=@sum(ms:x);
@for(lx(j):@sum(ms(i):c(i,j)*x(i))>b(j));
@for(ms:@gin(x));
end

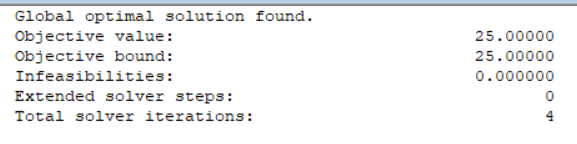
image-20200719170636707

按模式2切割15根，按模式5切割5根，按模式7切割5根，共25根，余料35米

3.2招聘问题

某服务部门一周中每天需要不同数目的雇员，周一到周四每天至少需要50人，周五至少需要80人，周六和周日至少需要90人，规定应聘者需连续工作5天，试确定聘用方案。

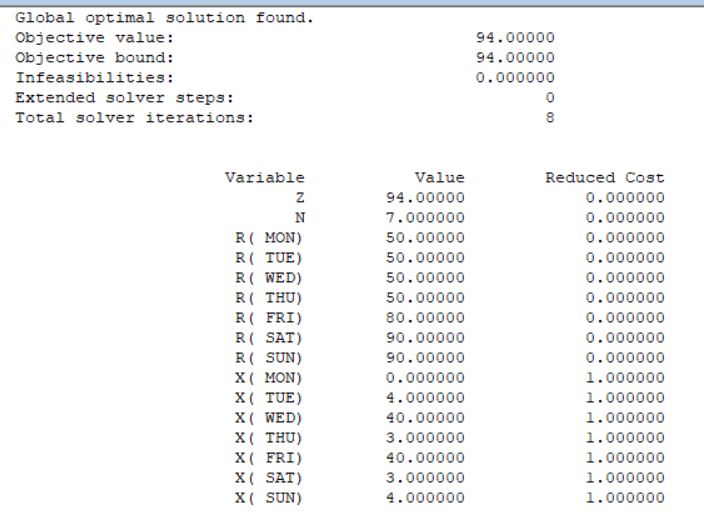
解： 周一至周日分别聘用xi个人上班，i =1,2,…,7，最少所需人数为Ri，总人数为z。

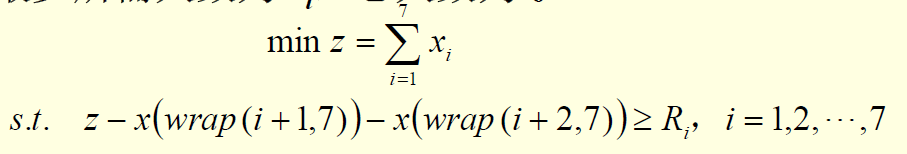
image-20200719171830766

由于连续工作五天，也就是这周一工作的时候上周一和周二的人就不要了，所以取余数。

根据模型编写Lingo代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
MODEL:
SETS:
DAYS/MON..SUN/:R,X;
ENDSETS
DATA:
R=50 50 50 50 80 90 90;
ENDDATA
MIN=Z;
N=@SIZE(DAYS);!集合的长度;
Z=@SUM(DAYS:X);
@FOR(DAYS(I):Z-X(@WRAP(I+1,N))-X(@WRAP(I+2,N))>R(I));
!@WRAP()相当于求余数，返回1到N之间的数;
@FOR(DAYS:@GIN(X));
END

image-20200719194902614

3.3人员安排问题(经典)

某班准备从5名队员中选４人组成接力队，参加学校的4×100m混合泳接力比赛，5名队员4种泳姿的百米平均成绩如表，问如何选拔队员。

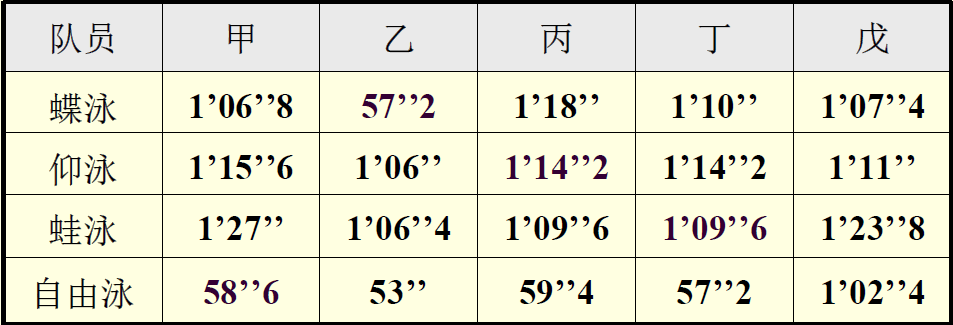
image-20200719194953630

经典0-1规划问题，设xij: 第i个泳姿由第j个人游（1—游，0—不游）

cij: 第i个泳姿由第j个人游的成绩，i=1,2,3,4； j=1,2,3,4,5

image-20200719195148797

根据模型编写Lingo代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
model:
sets:
swim/1..4/;
member/1..5/;
match(swim,member):c,x;
endsets
data:
c=66.8 57.2 78 70 67.4
75.6 60.6 74.2 74.2 71
87 66.4 69.6 69.6 83.8
58.6 53 59.4 57.2 62.4;
enddata
min=@sum(match:c*x);
@for(swim(i):@sum(member(j):x(i,j))=1);
@for(member(j):@sum(swim(i):x(i,j))<1);
@for(match:@bin(x));
end

image-20200719195804764

image-20200719195813256

3.4选址问题

某公司拟定在和平、南开、河东建立专卖店，拟议有7个地址：乐宾A1、劝业场A2、百货大楼A3，鼓楼A4、五马路A5，万达A6、爱琴海A7。并规定：和平(前三个)至多2个，南开(A4、A5)、河东(A6、A7)各至少1个，若选Ai，需投资bi元，每年可获利ci元，总投资不超过b元，如何选址使得公司的年利润最大？

image-20200719200155954

3.5面试顺序问题(经典)

有4名同学到一家公司参加3个部门的面试，公司要求每个同学面试必须先到秘书处，再到主管处，最后到经理处，并且不允许插队，由于4名同学的专业背景不同，所以每人在三个部门的面试时间也不同。这4名同学约定他们全部面试完以后一起离开公司，假定现在时间是早
上8：00，请问他们最早何时能离开公司？

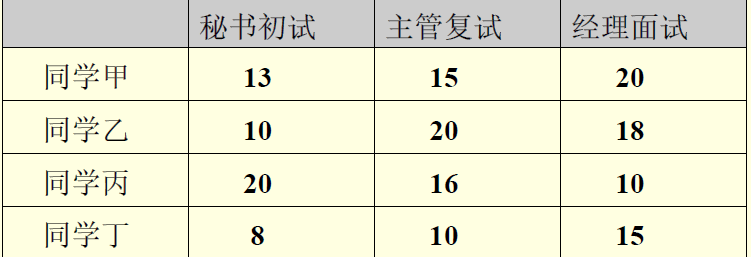
image-20200720101758099

解：设xij: 第i个同学到第j个部门面试开始的时刻，tij: 第i个同学在第j个部门面试的时间，i=1,2,3,4； j=1,2,3。

则xij+ tij: 第i个同学到第j个部门面试结束的时刻，T: 4人完成全部面试所花费的时间image-20200720101857319

image-20200720101928614

但是实际我们并不知道到底i和k谁先面试，约束条件在程序中也不好表示。由于这两式是互逆的，有且仅有一个成立，利用0-1
变量，把上式改写为image-20200720102129347

image-20200720102153405

根据模型编写Lingo代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
model:
sets:
stu/1..4/;
off/1..3/;
link1(stu,off):x,t;
link2(stu,stu)|&1#lt#&2:y;
!|&1#lt#&2表示i<j，说明是上三角矩阵;
endsets
data:
t=13 15 20
10 20 18
20 16 10
8 10 15 ;
enddata
min=time;
!time大于每名同学最后面试完毕时间;
@for(stu(i):time>x(i,3)+t(i,3));
!面试先后次序约束;
@for(link1(i,j)|j#le#2:x(i,j)+t(i,j)<x(i,j+1));
!每个阶段只能面试一个同学,y(i,k)=1表示第k名同学排在第i名同学前面,取M=1000;
@for(link1(i,j):@for(stu(k)|k#gt#i:x(i,j)+t(i,j)<x(k,j)+1000*y(i,k)));
@for(link1(i,j):@for(stu(k)|k#gt#i:x(k,j)+t(k,j)<x(i,j)+1000*(1-y(i,k))));
!定义0-1变量,最后通过0-1变量可以查看面试顺序;
@for(link2:@bin(y));
end

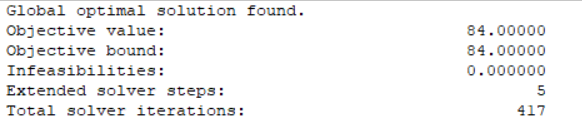
image-20200720102330790

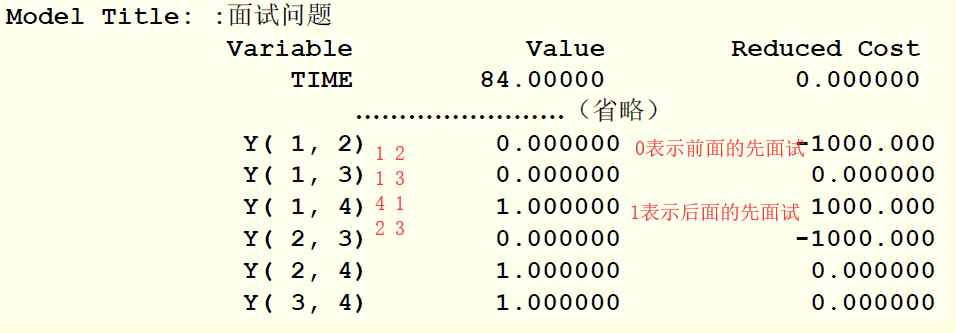
image-20200720102456879

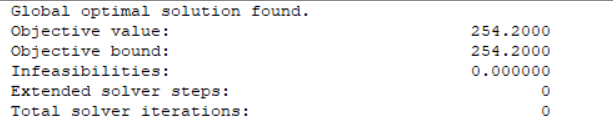
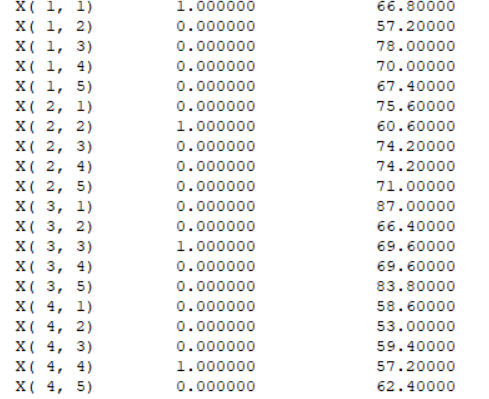
面试完成至少需要84min
面试顺序为4-1-2-3（丁-甲-乙-丙）

4.模糊线性规划

普通线性规划约束条件和目标函数都是确定的，但在一些实际问题中，约束条件可能带有弹性，目标函数可能不单一，价值系数可能带有模糊性。这些问题可以用模糊的方法来处理。

约束条件带有弹性的模糊线性规划为：

image-20200720110105513

理论在此不过多赘述，我们通过实际问题求解来看模糊线性规划问题的解题思路。

image-20200720105905791

1、首先求解普通线性规划

image-20200720110223945

2、其次，解如下有伸缩指标的普通线性规划

image-20200720110338564

3、最后，添加新的变量λ，求解普通线性规划

image-20200720110645755

作业

1.练习一

两个工厂A、B的产量都是10万个，三个仓库 x、y、z，产品都先送到仓库。四个顾客甲、乙、丙、丁，需求量分别为3、5、4、5万个。工厂到仓库、仓库到顾客的运费单价（元/个）如下。求总运费最少的运输方案。

A B 甲 乙 丙 丁
x 4 3 5 7 10 20
y 2 1 9 6 7 15
z 5 2 20 6 7 4

1595130571606

根据模型写出Lingo代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
model:
sets:
gc/1..2/:a;
ck/1..3/;
gk/1..4/:b;
link1(ck,gk):c,x;
link2(gc,ck):s,e;
endsets
data:
a=10 10;
b=3 5 4 5;
c=5 7 10 20 9 6 7 15 20 6 7 4;
s=4 2 5 3 1 2;
enddata
min=@sum(link2:e*s)+@sum(link1:x*c);
@for(gc(i):@sum(ck(j):e(i,j))<a(i));
@for(gk(j):@sum(ck(i):x(i,j))>b(j));
@for(ck(i):@sum(gk(j):x(i,j))<@sum(gc(j):e(j,i)));
end

运行结果：

image-20200719115144790

image-20200719115209134

2.练习二

连续投资10万元

A：从第1年 到第4年每年初要投资，次年末回收本利1.15

B：第3年初投资，到第5年末回收本利1.25，最大投资4万元

C：第2年初投资，到第5年末回收本利1.40，最大投资3万元

D：每年初投资，每年末回收本利1.11。

求：5年末总资本的最大值以及投资方案。

解： 假设：每年末总资产额 = 下年初的总投资额

​ 连续投资10万 = 第一年初的总投资额，连续指对各项目都可以投资

这个假设很重要，
若 不复投， 则过于简单；
若 每年末总资产额 > 下年初的总投资额，则过于复杂，做不出来，
若 连续投资10万 = 连续5年投资，很复杂，也做不出来

模型一：

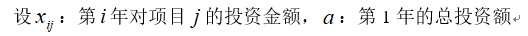
image-20200719133526031

建立数学模型：

image-20200719133741687

根据模型编写Lingo代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
model:
data:
a=100000;
enddata
max=1.15*x41+1.4*x23+1.25*x32+1.11*x54;
x11+x14=a;
x21+x23+x24=1.11*x14;
x23<30000;
x31+x32+x34=1.15*x11+1.11*x24;
x32<40000;
x41+x44=1.15*X21+1.11*x34;
x54=1.15*x31+1.11*x44;
end

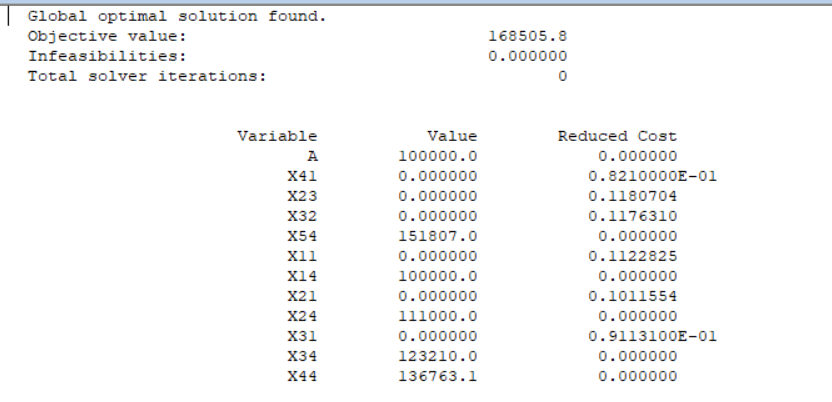
image-20200719133818615

模型二：比较复杂，决策变量增多，但是有推广性，可以延申到10年、20年……

image-20200719124641791

image-20200719133321491

根据模型编写Lingo代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
model:
sets:
year/1..5/:a,b;
obj/1..4/:p;
link(year,obj):x;
endsets
data:
p=1.15 1.25 1.4 1.11;
n=10;
enddata
max=b(5);
@for(year(i):a(i)=@sum(obj(j):x(i,j)));
@for(year(i)|i#ne#1#and#i#ne#5:b(i)=p(1)*x(i-1,1)+p(4)*x(i,4));
b(1)=p(4)*x(1,4);
b(5)=p(1)*x(4,1)+p(2)*x(3,2)+p(3)*x(2,3)+p(4)*x(5,4);
@for(year(i)|i#ne#2:x(i,3)=0);
@for(year(i)|i#ne#3:x(i,2)=0);
@for(obj(j)|j#ne#4:x(5,j)=0);
a(1)<n;
@for(year(i)|i#ne#1:a(i)=b(i-1));
x(3,2)<4;
x(2,3)<3;
end

image-20200719133923483

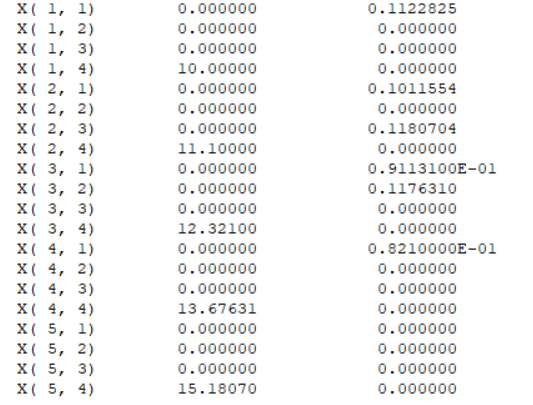
image-20200719133935157

由上表可知，要使第五年末总资本达到最大值168 505.8元，则

第一年初对D项目投资100 000元，

第二年初对D项目投资111 000元，

第三年初对D项目投资123 210元，

第四年初对D项目投资136 763.1元，

第五年初对D项目投资151 807元。

结语

我没什么才艺，给大家跳段街舞ጿኈቼዽጿኈቼዽጿኈቼዽጿኈቼዽጿኈቼዽጿዽጿኈቼዽጿኈቼዽጿኈቼዽጿኈቼዽጿኈቼዽጿኈቼዽጿኈቼዽጿኈቼዽጿኈቼዽጿኈቼዽጿኈቼዽጿኈቼዽጿኈቼዽ

赏

谢谢你请我吃糖果

支付宝
微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

很惭愧<br><br>只做了一点微小的工作<br>谢谢大家