EverydayOneCat
💯💯!

知识点
1.偏最小二乘回归介绍
偏最小二乘回归(PLS-Partial Least Squares)是一种新型的多元统计数据分析方法,是一种多因变量对多自变量的回归建模方法,是对最小二乘方法的推广。
优点:
1)提供了一种多因变量对多自变量的回归建模方法;
2)有效地解决变量之间的多重共线性问题;
3)适合当样本点数量少于自变量个数时进行回归建模;
4)最终模型中含原有所有自变量,回归系数容易解释。
5)计算简单、预测精度高,易于定性解释。
偏最小二乘回归≈主成分分析+典型相关分析+多元回归
2.偏最小二乘回归法的建模
(1)建立回归方程进行共线性检验
(2)若存在共线性,进行偏最小二乘回归
(3)确定成分个数
(4)建立偏最小二乘回归模型,进行解释
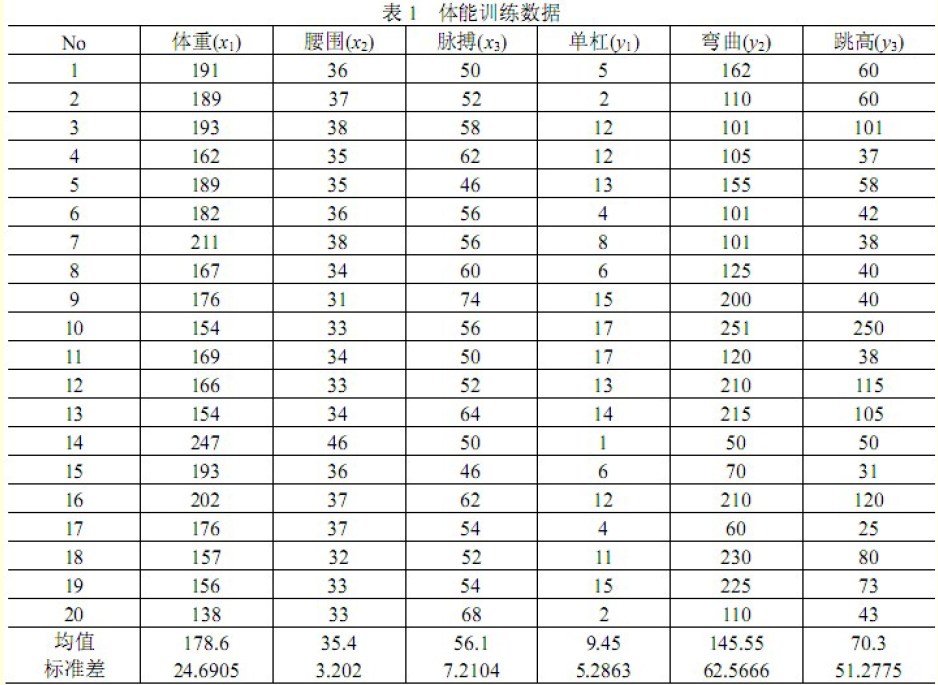
例:某康复俱乐部对20名中年人测量了
三个生理指标:体重x1, 腰围x2, 脉搏x3
三个训练指标: 单杠y1, 弯曲y2, 跳高y3
试用偏最小二乘回归建立由三个生理指标分别预测三个训练指标的回归模型。
SAS代码:
1 | data example; |
相关系数矩阵:

1.体重和腰围正相关; 2.体重、腰围与脉搏负相关;
3.单杠、跳高、弯曲的训练成绩与体重、腰围负相关,与脉搏正相关
用交叉验证法确定提取成分个数:
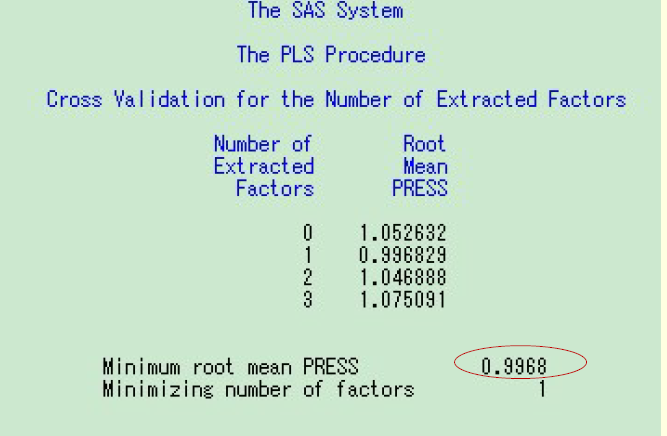
由结果可知,采用舍一交叉验证法提取1个成分,可使得PRESS最小

提取的1个成分解释自变量的比率为69.4781%,解释因变量的比率为20.9447%。
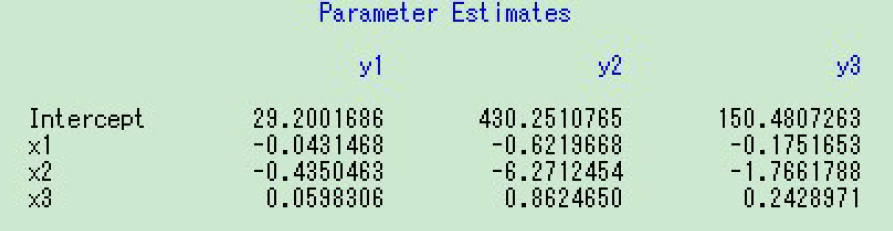
标准化模型参数估计:
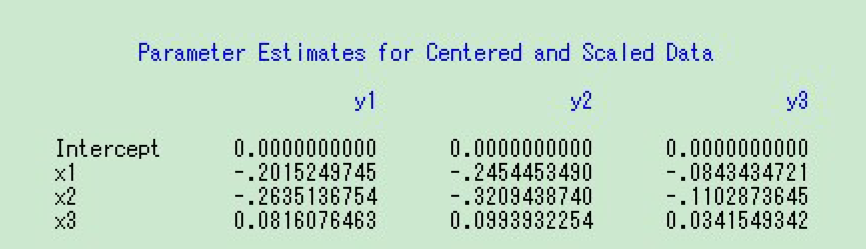
由表可写出标准化变量的回归方程,结果如下:
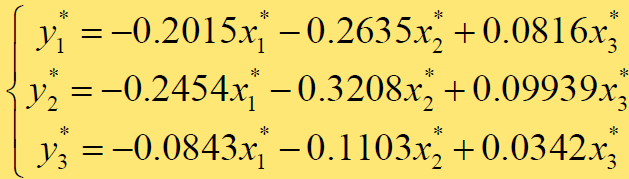
原始模型的参数估计:
还原成原始变量的回归方程,结果如下:
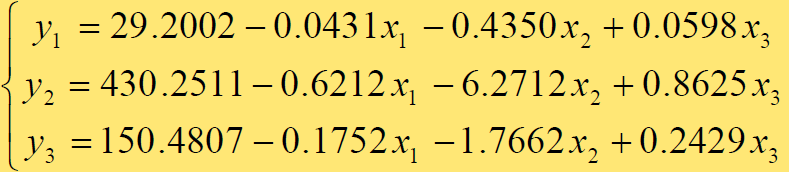
作业
下列数据是2个因变量和6个自变量。请用偏最小二乘回归建立方程组,并预测最后四个数的因变量值。
| Y1 | Y2 | X1 | X2 | X3 | X4 | X5 | X6 |
|---|---|---|---|---|---|---|---|
| 1394.89 | 2505 | 519.01 | 8144 | 373.9 | 117.3 | 112.6 | 843.43 |
| 920.11 | 2720 | 345.46 | 6501 | 342.8 | 115.2 | 110.6 | 582.51 |
| 2849.52 | 1258 | 704.87 | 4839 | 2233.3 | 115.2 | 115.8 | 1234.85 |
| 1092.48 | 1250 | 290.90 | 4721 | 717.3 | 116.9 | 115.6 | 697.25 |
| 832.88 | 1387 | 250.23 | 4134 | 781.7 | 117.5 | 116.8 | 419.39 |
| 2793.37 | 2397 | 387.99 | 4911 | 1371.1 | 116.1 | 114.0 | 1840.55 |
| 1129.20 | 1872 | 320.45 | 4430 | 497.4 | 115.2 | 114.2 | 762.47 |
| 2014.53 | 2334 | 435.73 | 4145 | 824.8 | 116.1 | 114.3 | 1240.37 |
| 2462.57 | 5343 | 996.48 | 9279 | 207.4 | 118.7 | 113.0 | 1642.95 |
| 5155.25 | 1926 | 1434.95 | 5943 | 1025.5 | 115.8 | 114.3 | 2026.64 |
| 3524.79 | 2249 | 1006.39 | 6619 | 754.4 | 116.6 | 113.5 | 916.59 |
| 2003.58 | 1254 | 474.00 | 4069 | 908.3 | 114.8 | 112.7 | 824.14 |
| 2003.58 | 1254 | 474.00 | 4069 | 908.3 | 114.8 | 112.7 | 824.14 |
| 2160.52 | 2320 | 553.97 | 5857 | 609.3 | 115.2 | 114.4 | 433.67 |
| 1205.11 | 1182 | 282.84 | 4211 | 411.7 | 116.9 | 115.9 | 571.84 |
| 5002.34 | 1527 | 1229.55 | 5154 | 1196.6 | 117.6 | 114.2 | 2207.69 |
| 3002.74 | 1034 | 670.35 | 4344 | 1574.4 | 116.5 | 114.9 | 1367.92 |
| 2391.42 | 1527 | 571.68 | 4685 | 849.0 | 120.0 | 116.6 | 1220.72 |
| 2195.70 | 1408 | 422.61 | 4797 | 1011.8 | 119.0 | 115.5 | 843.83 |
| 5381.72 | 2699 | 1639.83 | 8250 | 656.5 | 114.0 | 111.6 | 1396.35 |
| 1606.15 | 1314 | 382.59 | 5105 | 556.0 | 118.4 | 116.4 | 554.97 |
| 364.17 | 1814 | 198.35 | 5340 | 232.1 | 113.5 | 111.3 | 64.33 |
| 3534.00 | 1261 | 822.54 | 4645 | 902.3 | 118.5 | 117.0 | 1431.81 |
| 630.07 | 942 | 150.84 | 4475 | 301.1 | 121.4 | 117.2 | 324.00 |
| 1206.68 | 1261 | 334.00 | 5149 | 310.4 | 121.3 | 118.1 | 716.65 |
| 55.98 | 1110 | 17.87 | 7382 | 4.2 | 117.3 | 114.9 | 5.57 |
| 1000.03 | 1208 | 300.27 | 4396 | 500.9 | 119.0 | 117.0 | 600.98 |
| 114.81 | 5493 | 507.0 | 119.8 | 116.5 | 468.79 | ||
| 47.76 | 5753 | 61.6 | 118.0 | 116.3 | 105.80 | ||
| 61.98 | 5079 | 121.8 | 117.1 | 115.3 | 114.40 | ||
| 376.95 | 5348 | 339.0 | 119.7 | 116.7 | 428.76 |
调用SAS 软件中的pls 函数作偏最小二乘回归,SAS代码如下:
1 | data ex; |
用交叉验证法确定提取成分个数:
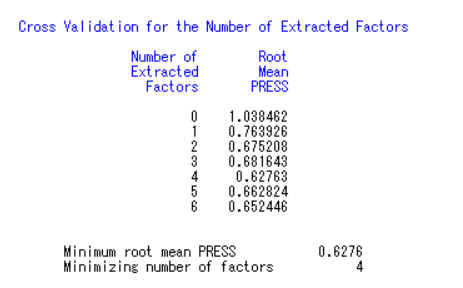
提取4 个成分可使得PRESS 最小。
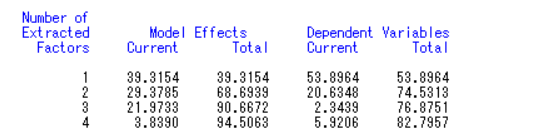
提取的4 个成分解释自变量的比率为94.5063%,解释因变量的比率为82.7957%,说明建模效果较好。
原模型的参数估计:

根据分析结果,可得到原始变量的回归方程。
𝑦1 = −2598.08360 + 2.92088𝑥1 − 0.05099𝑥2 + 0.38517𝑥3 − 55.58412𝑥4 + 80.15261𝑥5 + 0.42225𝑥6
𝑦2 = 12626.50026 − 0.59073𝑥1 + 0.37517𝑥2 − 0.19742𝑥3 + 52.63768𝑥4 − 167.85207𝑥5 + 0.74289𝑥6
1 | data ex; |

对模型做残差检验,得到y1 和y2 的总残差分别为1985848.01、6386427.07,故此模型拟合不佳。
预测结果

结语
今晚IG打RNG,芜湖春晚又到了。我已经开始唱了你们呢:难忘~今宵~难忘今宵~~


