数学建模—岭回归

EverydayOneCat

⛽️！！

知识点

1.笔记

2.用岭回归选择变量

岭回归选择变量的原则：

（1）可以剔除掉标准化岭回归系数比较稳定且绝对值很小的自变量。
（2）随着k的增加，回归系数不稳定，震动趋于零的自变量也可以剔除。
（3）有若干个回归系数不稳定，去掉几个，去掉哪几个，需根据去掉某个变量后重新进行岭回归分析的效果来确定。

例：空气污染问题。Mcdonald 和Schwing 曾研究死亡率与空气污染、气候以及社会经济状况等因素的关系。考虑了15个解释变量，收集了60组样本数据。

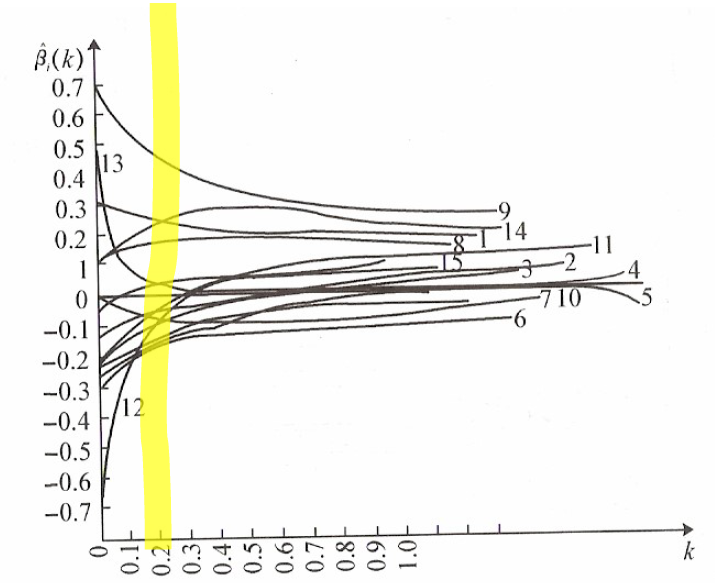
把15个回归系数的岭迹画到图中，我们可看到，当k=0.20时岭迹大体上达到稳定。按照岭迹法，应取k=0.2。

若用方差扩大因子法，因k=0.18时，方差扩大因子接近于1，当k在0.02～0.08时，方差扩大因子小于10，故应建议在此范围选取k。

从岭迹看到自变量x4,x7,x10,x11和x15有较稳定且绝对值比较小的岭回归系数，根据变量选择的第一条原则，这些可以去掉。
又因为自变量x12和x13的岭回归系数很不稳定，且随着k的增加很快趋于零，根据上面的第二条原则，也应该去掉。
再根据第三条原则去掉变量x3和x5。

这个问题最后剩的变量是x1，x2，x6，x8，x9，x14。

3.岭回归的应用

以民航客运量模型为例

3.1多元线性回归模型的建立

第一步，提出因变量与自变量，收集数据

SAS程序如下：

data sj; 
input time y x1-x5@@; /*@@:指针控制符，读取下面数据时自动换行*/
card;
… 省略号部分录入数据
;
run;

第二步，Pearson相关系数检验

proc corr data=sj; /*proc: 过程步的开始，表示调用;corr: 相关系数矩阵*/
var y; 
with x1 x2 x3 x4 x5; /*with 表示y和这些，不加的话就是两两相比较*/
run;

说明x3和y没有信息传递。

第三步，做回归分析，输出结果

proc reg data=sj; 
model y=x1 x2 x3 x4 x5; /*reg: 线性回归*/
run;

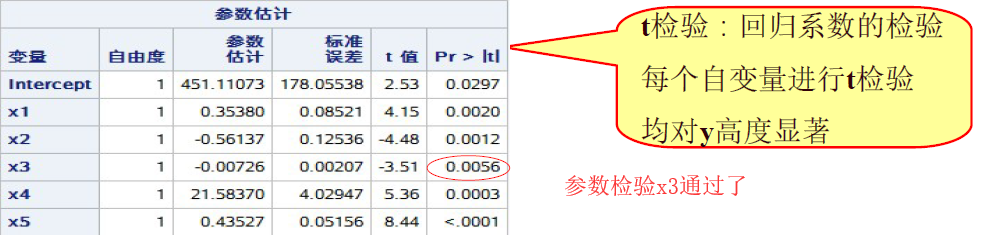
由此写出回归方程：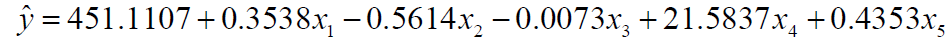

第四步，回归诊断

(1) 拟合优度检验

(2) F检验

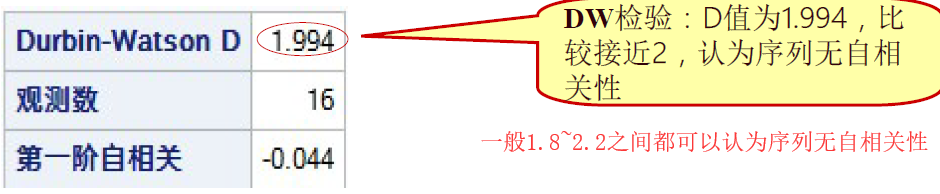
第五步，DW检验，检验随机项的一阶自相关性

proc reg data=sj; 
model y=x1 x2 x3 x4 x5/dw; /*dw: DW检验*/
run;

3.2岭回归模型的建立

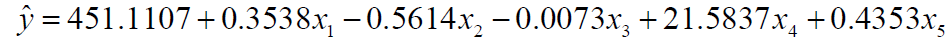
x2的回归系数-0.5614 是负的， x2是消费额，负的回归系数显然是不合理的，其原因可能是自变量间存在共线性，因而回归方程需要进行改进。下面，采用岭回归的方法进行改进，具体步骤如下:

第一步，提出因变量与自变量，收集数据

第二步，多重共线性检验

proc reg data=sj; 
model y=x1-x5/vif collin collinoint;
/*vif: 方差膨胀因子;collin：对截距项未校正共线性诊断;collinoint：对截距项校正的共线性诊断*/
run;

（1）方差膨胀因子法

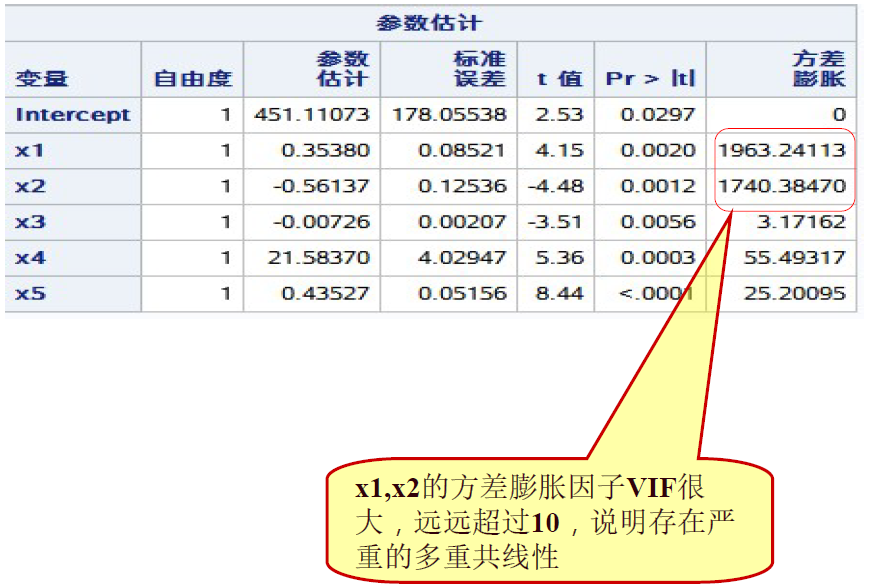
（2）条件指数

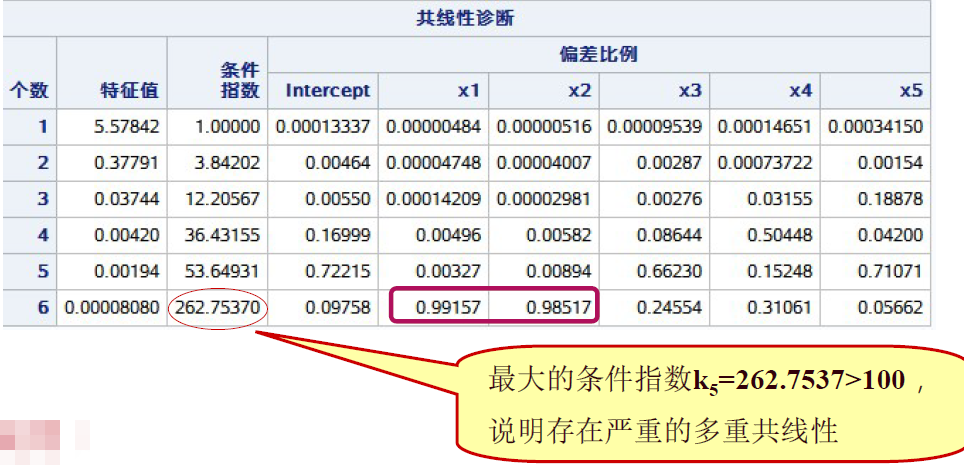
说明：
(1) 特征值是从大到小排的，不是按自变量的顺序排列的
(2) 通过右侧的方差比例粗略判断自变量间的多重共线性

第三步，数据标准化

proc standard data=sj /*standard: 对数据进行标准化，*/
m=0 s=1 out=sj2; /*并输出到新的数据集sj2;m=0: 均值为0;s=1: 标准差为1*/
run;

第四步，实现岭回归

proc reg data= sj2 outest= outest 
graphics outvif; /*graphics : 画出高分辨的图形;outvif: 输出方差膨胀因子*/
ridge=0 to 1.0 by 0.05; /*岭参数k在0～1范围内，步长0.05*/
model y= x1 x2 x3 x4 x5;
run;

第五步，绘制岭迹图

plot /ridgeplot;/*绘制岭迹图*/ 
run；

第六步，打印岭回归参数估计结果

proc print data =outest; /*打印模型的参数*/
run;

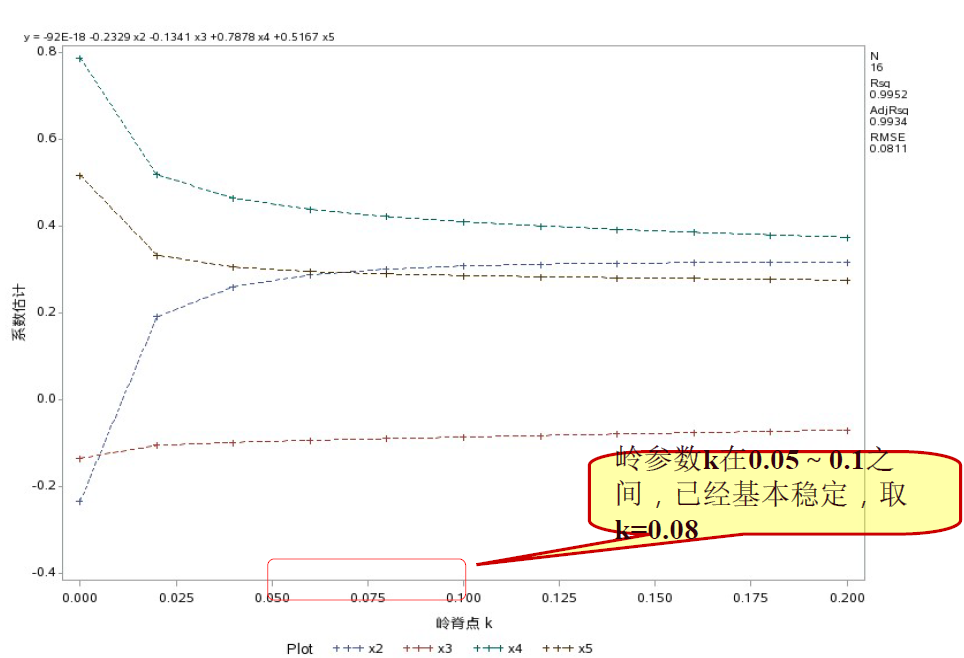
岭迹图分析：

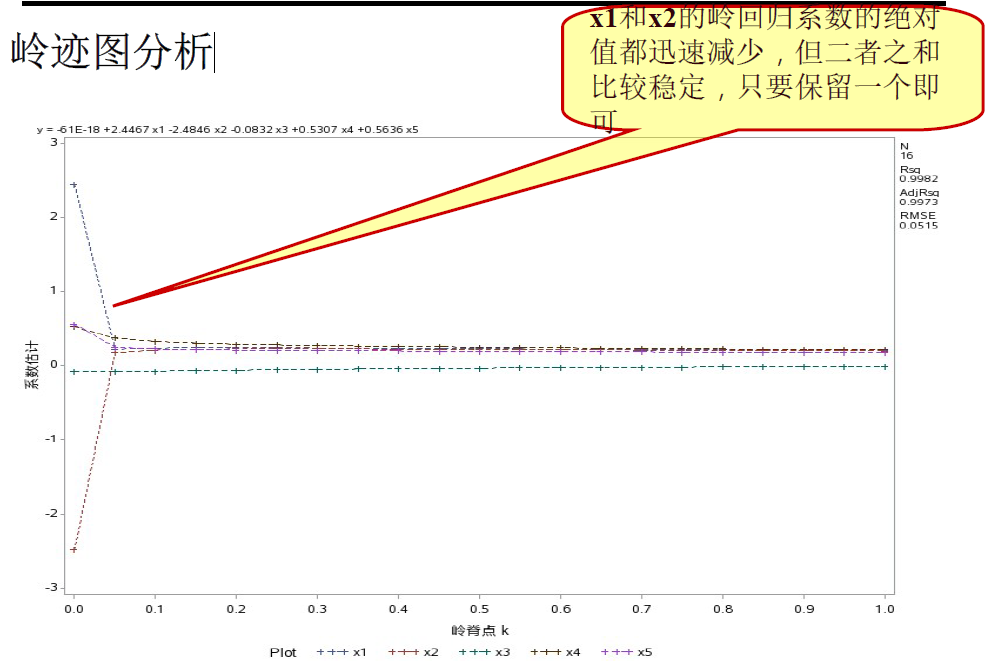
通过上面的分析，我们决定剔除x1，用y与其余4个变量重新做岭回归。把岭参数步长改为0.02，范围减小到0.2。结果如下：

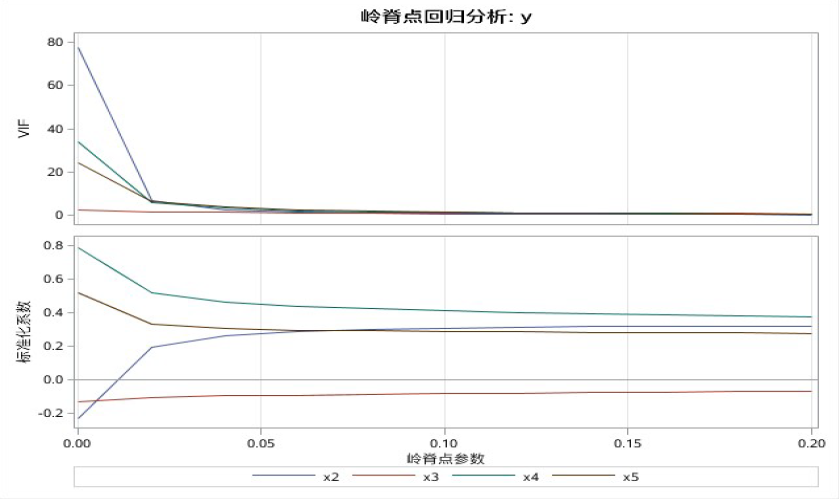
岭回归数据集：

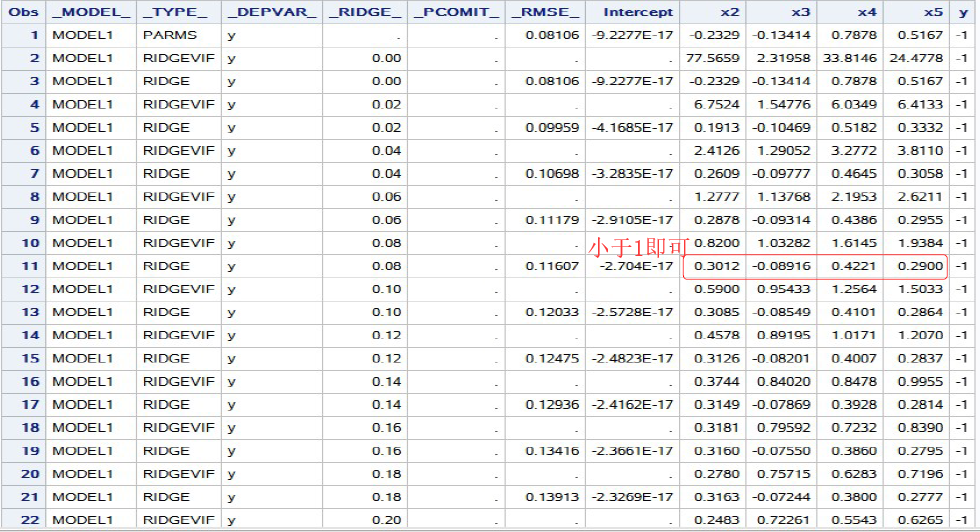
标准化岭回归方程：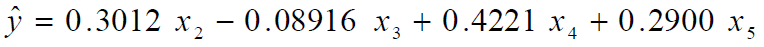

原变量岭回归方程：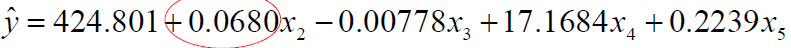

作业

一家大型商业银行有多家分行，近年来，该银行的贷款额平稳增长，但不良贷款额也有较大比例的提高。为弄清楚不良贷款形成的原因，希望利用银行业务的有关数据做定量分析，以便找出控制不良贷款的办法。

(1) 计算y与其余4个变量的简单相关系数；

(2) 建立不良贷款y对4个变量的线性回归方程，所得的回归系数是否合理?

(3) 分析回归模型的共线性；

(4) 建立不良贷款y对4个变量的岭回归；

(5) 某研究人员希望做y对各项贷款余额、本年累计应收贷贷款、贷款项目个数这3个自变量的回归，你认为这样做是否可行？如果可行应该如何做？

分行编号	不良贷款 y(亿元)	各项贷款余额 x1(亿元)	本年累计应收 贷款x2(亿元)	贷款项目个数 x3(个)	本年固定资产 投资额x4(亿元)
1	0.9	67.3	6.8	5	51.9
2	1.1	111.3	19.8	16	90.9
3	4.8	173.0	7.7	17	73.7
4	3.2	80.8	7.2	10	14.5
5	7.8	199.7	16.5	19	63.2
6	2.7	16.2	2.2	1	2.2
7	1.6	107.4	10.7	17	20.2
8	12.5	185.4	27.1	18	43.8
9	1.0	96.1	1.7	10	55.9
10	2.6	72.8	9.1	14	64.3
11	0.3	64.2	2.1	11	42.7
12	4.0	132.2	11.2	23	76.7
13	0.8	58.6	6.0	14	22.8
14	3.5	174.6	12.7	26	117.1
15	10.2	263.5	15.6	34	146.7
16	3.0	79.3	8.9	15	29.9
17	0.2	14.8	0.6	2	42.1
18	0.4	73.5	5.9	11	25.3
19	1.0	24.7	5.0	4	13.4
20	6.8	139.4	7.2	28	64.3
21	11.6	368.2	16.8	32	163.9
22	1.6	95.7	3.8	10	44.5
23	1.2	109.6	10.3	14	67.9
24	7.2	196.2	15.8	16	39.7
25	3.2	102.2	12.0	10	97.1

1.第一问

调用SAS 软件中的corr 函数作相关性检验，SAS代码：

data ex;
input y x1-x4@@;
cards;
0.9	67.3	6.8	5	51.9
1.1	111.3	19.8	16	90.9
4.8	173.0	7.7	17	73.7
3.2	80.8	7.2	10	14.5
7.8	199.7	16.5	19	63.2
2.7	16.2	2.2	1	2.2
1.6	107.4	10.7	17	20.2
12.5	185.4	27.1	18	43.8
1.0	96.1	1.7	10	55.9
2.6	72.8	9.1	14	64.3
0.3	64.2	2.1	11	42.7
4.0	132.2	11.2	23	76.7
0.8	58.6	6.0	14	22.8
3.5	174.6	12.7	26	117.1
10.2	263.5	15.6	34	146.7
3.0	79.3	8.9	15	29.9
0.2	14.8	0.6	2	42.1
0.4	73.5	5.9	11	25.3
1.0	24.7	5.0	4	13.4
6.8	139.4	7.2	28	64.3
11.6	368.2	16.8	32	163.9
1.6	95.7	3.8	10	44.5
1.2	109.6	10.3	14	67.9
7.2	196.2	15.8	16	39.7
3.2	102.2	12.0	10	97.1
;
proc corr;
var y;with x1-x4;
run;

可以看出y 与其余4 个变量相关性的检验R 检验的概率均小于0.05，故拒绝xi(i=1,2,3,4)与y 无相关关系的原假设，即认为它们之间有明显的相关关系。

2.第二问

调用SAS 软件中的reg 函数作多元回归，SAS代码如下：

data ex;
input y x1-x4@@;
cards;
数据区
;
proc reg;model y=x1-x4/dw;
run;

其中F=19.70，P 值远小于0.05，故拒绝参数都为0的原假设，即认为y 与xi(i=1,2,3,4)之间具有显著的线性关系。

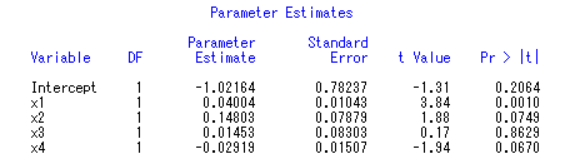
由图可知对系数及自变量x2、x3、x4，t 检验的Pr > |t|的概率均大于0.05，故接受参数为0的原假设，即认为系数及自变量x2、x3、x4 的系数未通过显著性检验。

逐步去除未通过t 检验的变量，得到最终结果如下表所示：

对自变量x1 和x4，t 检验的Pr > |t|的概率均小于0.05，故拒绝原假设，即认为自变量x1 和x4 的系数通过了显著性检验。

故回归方程为：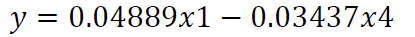

𝑥4的回归系数-0.03437 是负的， 𝑥4是本年固定资产投资额，负的回归系数显然是不合理的。其原因可能是自变量间存在共线性，因而回归方程需要进行改进。

DW检验比较接近2，认为序列无自相关性。

3.第三问

调用SAS 软件中的reg 函数作岭回归，SAS代码如下：

data ex;
input y x1-x4@@;
cards;
数据区
;
proc reg;model y=x1-x4/vif collin collinoint;
run;

方差膨胀因子法：

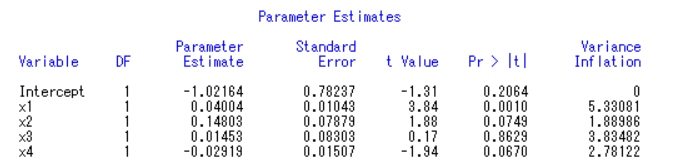
x1、x2、x3、x4 的方差膨胀因子都小于10，说明无多重共线性。

条件指数：

最大的条件指数为11.21475，小于100，说明无多重共线性。

4.第四问

SAS代码：

data ex1;
input y x1-x4@@;
cards;
数据区
;
proc reg data=ex1 outest=out2 graphics outvif;
model y=x1-x4/ridge=0.0 to 1.0 by 0.1;
plot/ridgeplot;
proc print data=out2;
run;

岭迹图：

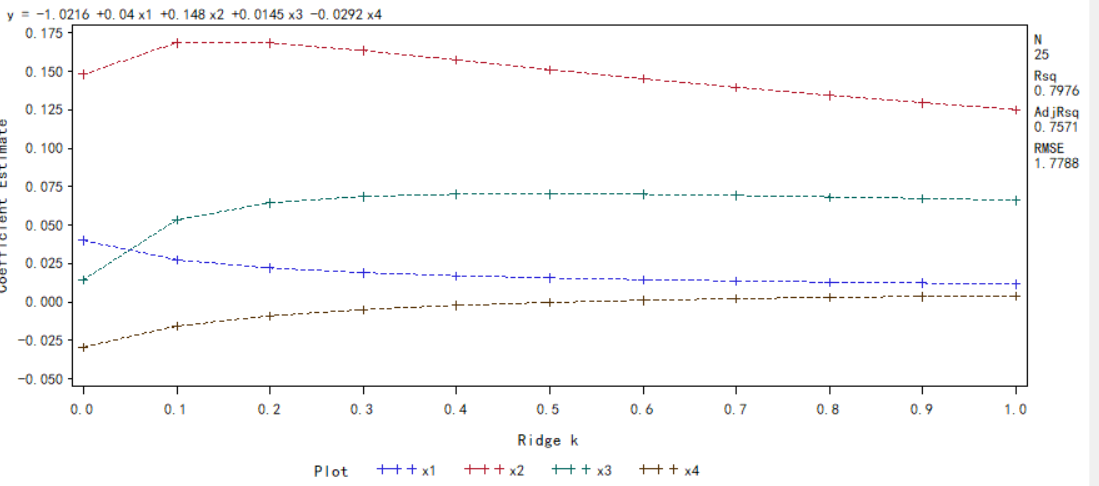
x1、x4 的岭回归系数趋于零，因此此变量不重要，可以去掉

当𝑘 ≥ 0.3后，各回归系数的岭迹曲线趋于稳定，故取𝑘 = 0.3的岭回归估计建立岭回归方程。

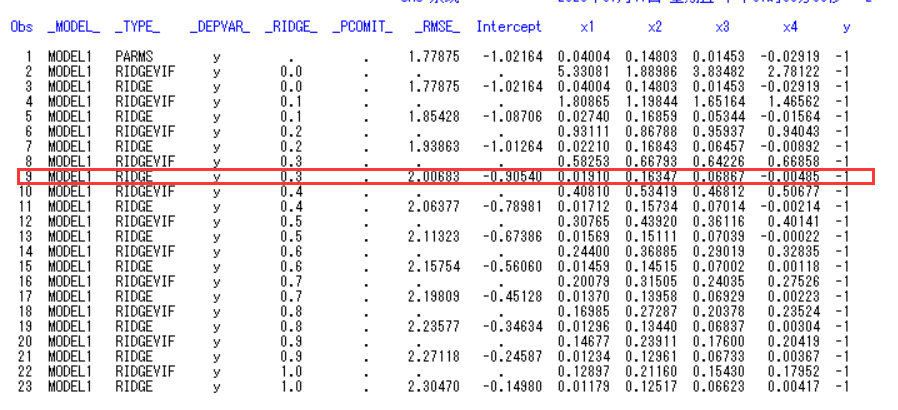
所以原变量岭回归程:

$$y=-0.90540+0.16347x2+0.006867x3$$

5.第五问

由以上得到，不可行，需要再去掉x1—— 各项贷款余额

结语

久违的一天两更，芜湖！

赏

谢谢你请我吃糖果

支付宝

微信