EverydayOneCat
📦🙀正方?圓滾?
🛏️💤🐈💨

知识点
1.笔记

2.两个正态总体的检验
例:某小麦品种经过4代选育,从第5代和第6代中分别抽出10株得到它们株高的观测值分别为66,65,66,68,62,65,63,66,68,62和64,61,57,65,65,63,62,63,64,60,试检验株高这一性状是否已达到稳定(α=0.05)?
思路:先检验方差后检验均值
SAS代码:
1 | data ex; |
ttest表示T检验,检验两个水平的,每个水平的都符合正态分布。
class表示分类变量(属性)
先看方差检验
Pr>F概率大于0.05,接受原假设H0:方差相等
再看均值检验
T检验概率比0.05小,拒绝原假设,认为两均值不等,第五代和第六代株高有显著性差异,说明株高性状没有达到稳定。
3.两组样本非参数检验
非参数检验(non-parametric test)又称为分布自由检验,一种与总体分布状况无关的检验方法,它不依赖于总体分布的形式。
3.1配对样本数据符号检验法
例1 甲乙两人分析同一物质中某成份的含量,得到观测数据(单位:g)为
甲14.7,15.0,15.2,14.8,15.5,14.6,14.9,14.8,15.1,15.0
乙14.6,15.1,15.4,14.7,15.2,14.7,14.8,14.6,15.2,15.0
试在显著性水平为0.05时用符号检验法检验两人的分析无显著差异.
SAS代码:
1 | data ex; /*ex为数据名*/ |
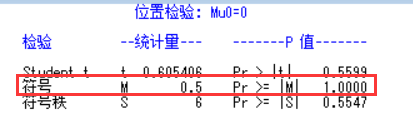
结果分析: 由Tests for Location: Mu0=0表可知,M(Sign)的值为05,pr>M的值为1.00>0.05,未落在拒绝域里,故接受原假设H,认为两人的分析无显著差异。
3.2总体中位数的符号检验法
为了判断某个总体的中位数是否与已知数m有显著的差异
例2 试验品种猪在17个试验点的月增重(单位:kg)见表: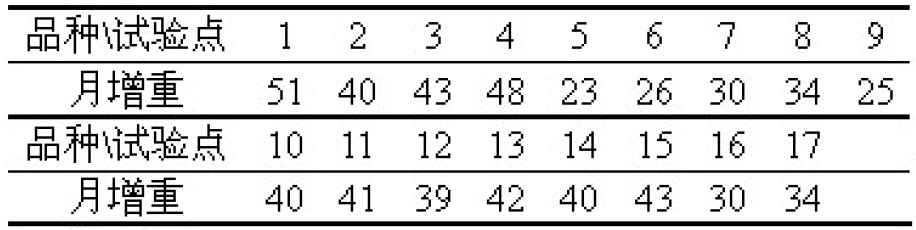
试问,月增重与35是否有显著性差异?
SAS代码:
1 | data ex; |
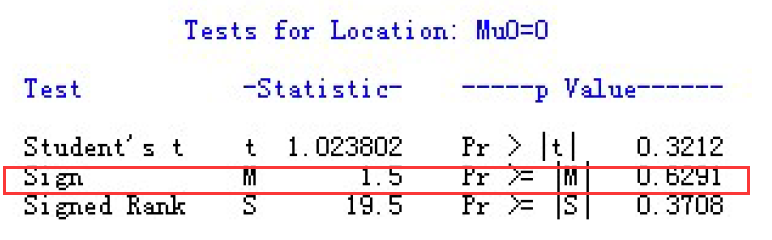
结果分析:M(Sign)的值为1.5,Pr >= |M|值为0.6291>0.05,故未落在拒绝域里,因此接受原假设,认为该品种猪月增重的中位数与35无显著差异。
3.3成组样本数据的秩和检验法
例3 测定两个马铃薯品种的淀粉含量(%),得到A品种的观测值为12.6, 12.4,B品种的观测值为12.4,12.1,12.5,12.7,12.6,13.1试在显著性水平为0.05时用秩和检验法检验两品种的淀粉含量无显著差异。
这里一个2个一个6个不是一一配对,我们用到秩和检验法。
SAS代码:
1 | data ex; |

结果分析:
Kruskal-Wallis Test这一部分,自由度DF为1,Chi-Square value 为Chi-Square且Prob > Chi-Square 为0.7358>0.05,接受原假设H0,认为两品种的淀粉含量没有显著性差异,淀粉含量相同。
4.单因素方差分析
例4《切胚乳试验》用小麦种子进行切胚乳试验,设计分3种处理,同期播种在条件较为一致的花盆内,出苗后每盆选留2株,成熟后测量每株粒重(单位:g),得到数据如下:
| 处理 | 每株粒重 |
|---|---|
| 未切去胚乳 | 21,29,24,22,25,30,27,26 |
| 切去一半胚乳 | 20,25,25,23,29,31,24,26,20,21 |
| 切去全部胚乳 | 24,22,28,25,21,26 |
分析粒重和处理方式是否有关。
SAS代码:
1 | data ex;do a=1 to 3;input n @@; |

根据此做出来表格:
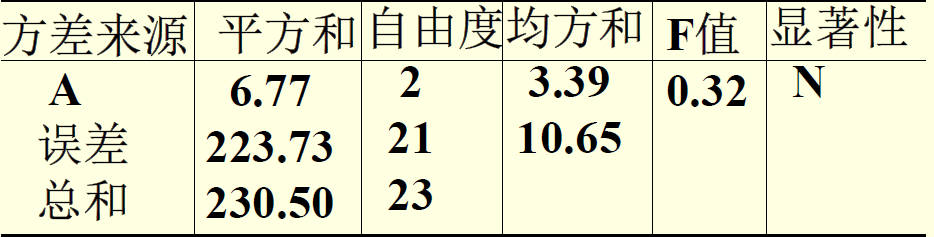
F值为0.32,Pr>F概率大于0.05,接受原假设:均值相等

都归属于A类,没有显著性差异,认为不同的处理方式对粒重并无明显影响。
5.双因素方差分析
5.1不考虑交互作用
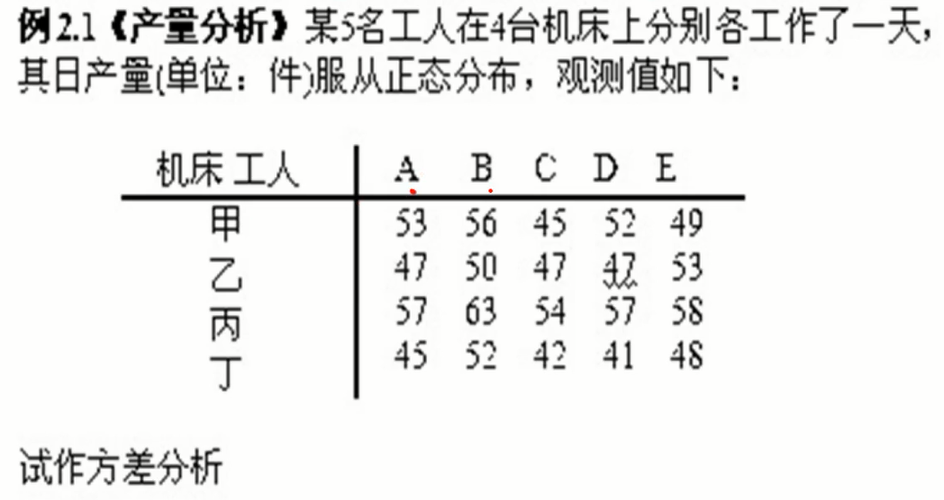
SAS代码:
1 | data ex;do a=1 to 4;do b=1 to 5; |
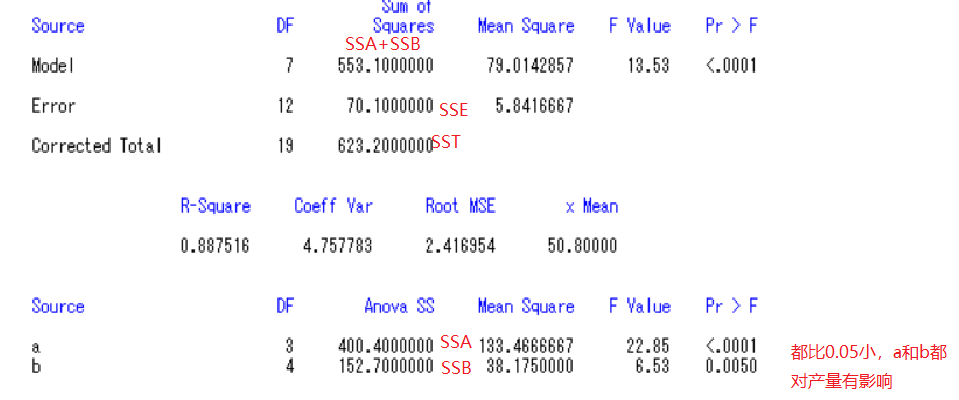
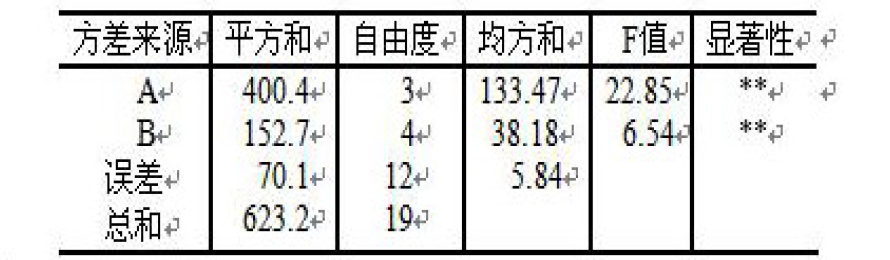
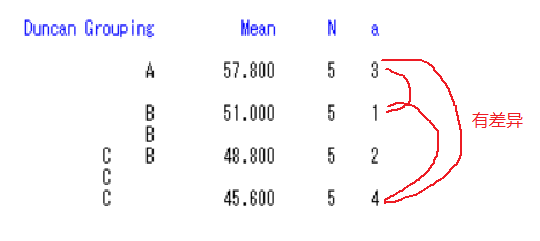
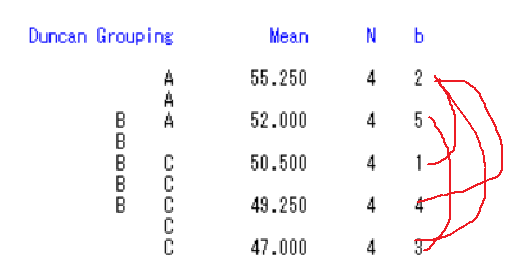
5.2考虑交互作用
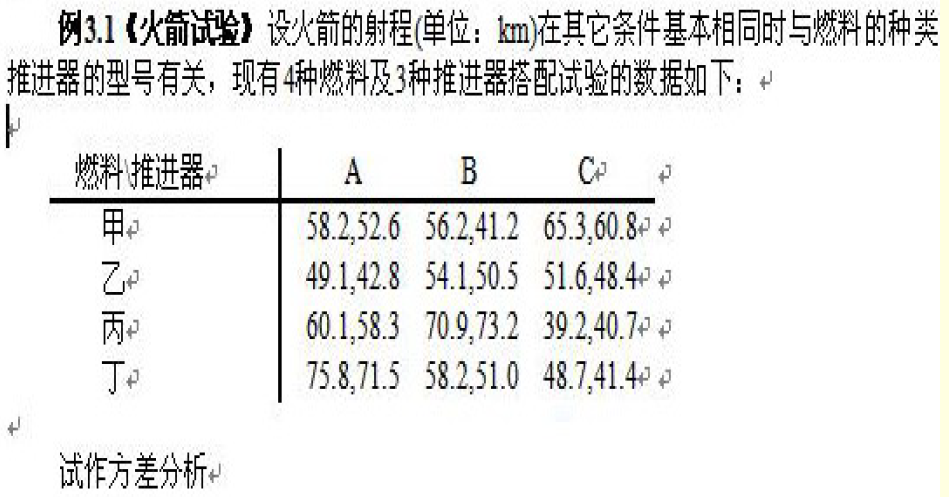
要是研究交互作用,每个交叉处至少有两个值。
1 | data ex;do a=1 to 4;do b=1 to 3;do i=1 to 2; |

6.多组独立样本的非参数检验
多组独立样本的H检验法(又称为Kruskal -Wallis单向秩次方差分析法),是检验多组独立样本是否来自同分布总体最常用、功效最强的非参数检验方法。
例 用3种不同的药剂处理水稻种子,发芽后观测到苗高(单位:cm)的观测值如下,试作单向秩次方差分析。

1 | data ex;do a=1 to 3; |
7.独立性检验

原假设H0:是否使用预防措施与患感冒情况相互独立。
编写程序如下:
1 | data ex;do a=1 to 2;do b=1 to 3; /*两行三列*/ |

第二部分Statistics for Table of a by b才是检验结果。其中主要看Chi-Square(卡方)这一行,其自由度为2,χ2(Chi-Square value)=7.5691,且Prob值为0.0227<0.05,故落在拒绝域,接受备择假设,即预防与感冒这两因素之间不是相互独立的,即措施对患感冒是有关系的。
8.协方差分析
如果在单因素、双因素或多因素试验中有无法控制的因素x影响试验的结果Y,且x可以测量、x与Y之间又有显著的线性回归时,常常利用线性回归来矫正Y的观测值、消去x的差异对Y的影响。
例如,研究施肥对苹果树产量的影响,由于苹果树的长势不齐,必须消去长势对产量的影响。又如,研究饲料对动物增重的影响,由于动物的初重不同,必须消去初重对增重的影响。
8.1单因素协方差分析

SAS代码:
1 | data ex; do a=1 to 3;do i=1 to 8; |
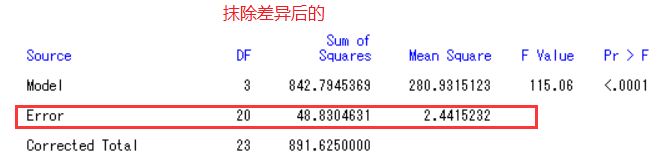
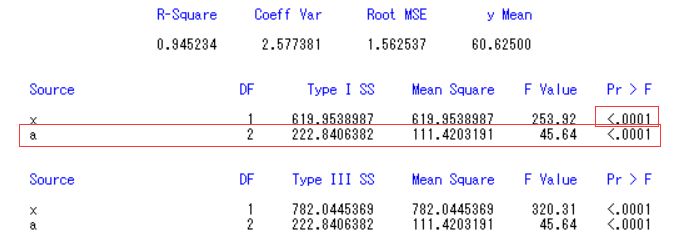
x对应的Pr>F概率小于0.05,拒绝原假设H0:x对y没有影响,说明x差异显著,所以我们要把x差异性抹掉。
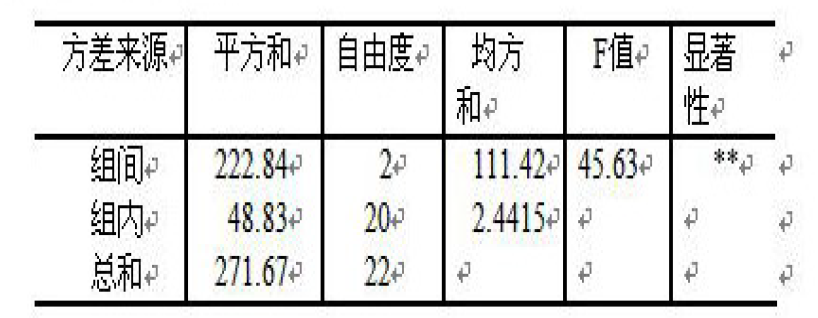
施用三种肥料的产量矫正后有极显著的差异(有影响)。
8.2双因素协方差分析
8.2.1不考虑交互作用
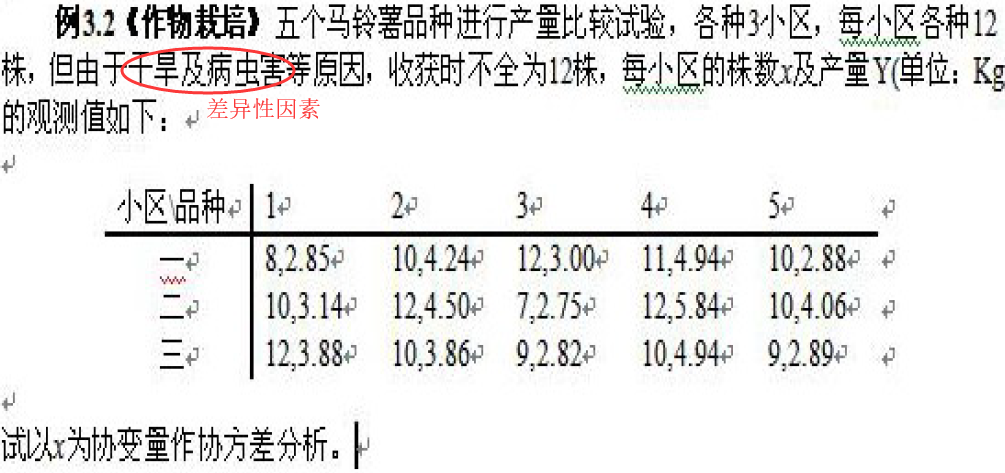
1 | data ex;do a=1 to 3 ;do b=1 to 5 ; |
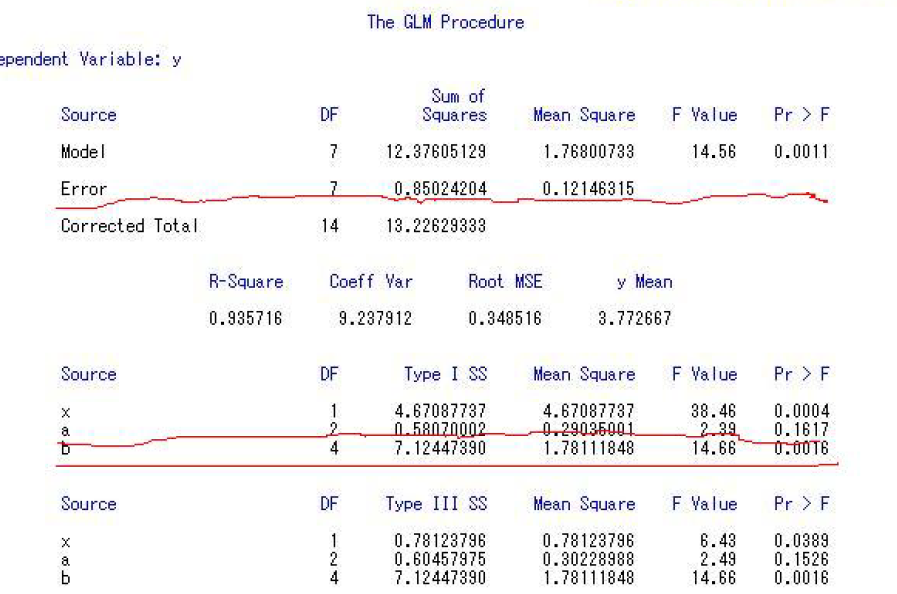
x对应的Pr>F概率小于0.05,差异性显著,所以要抹除x的影响。
a对应的Pr>F概率大于0.05,说明不同的小区对产量没有影响。
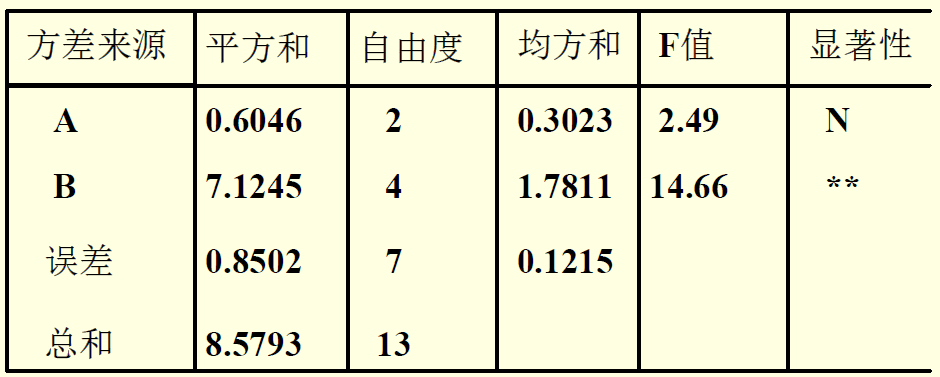
各小区的产量矫正后没有显著的差异,各品种的产量矫正后有极显著的差异。
8.2.2考虑交互作用
1 | data ex; do a=1 to 4; do b=1 to 2; |
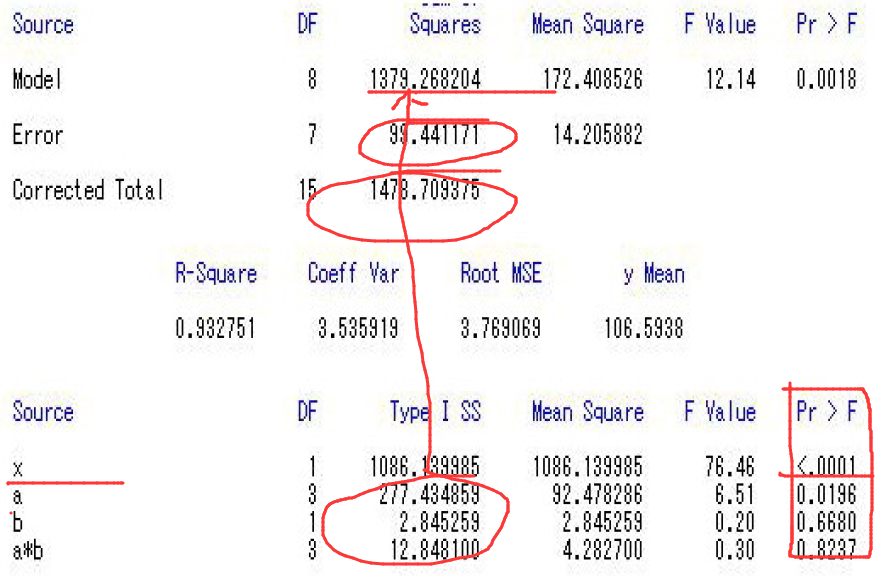
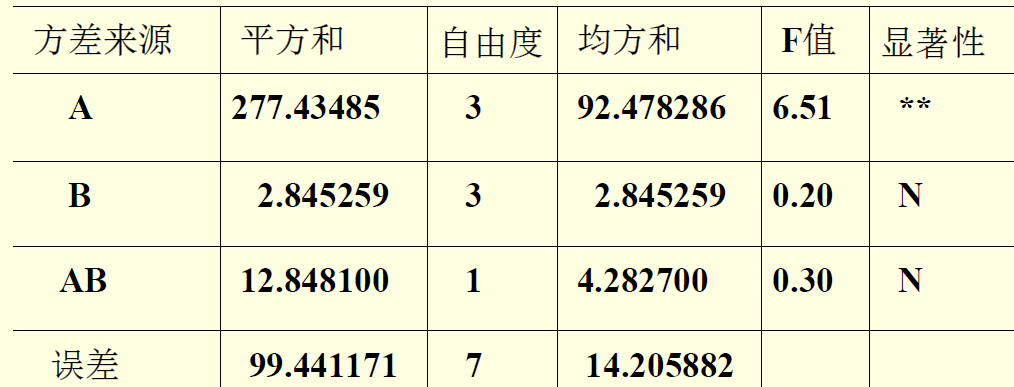
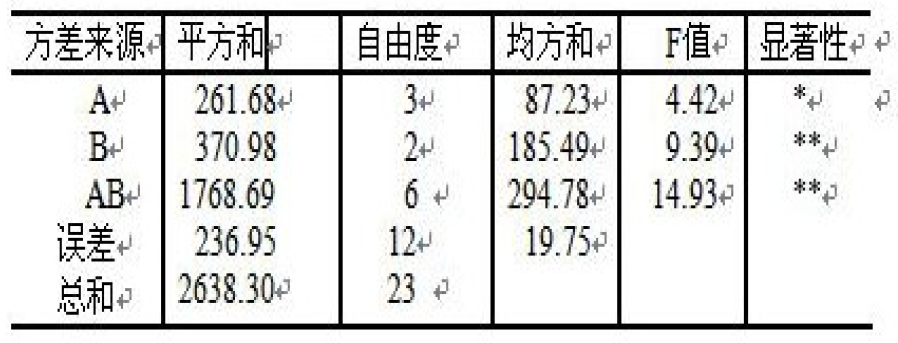
A与B的交互作用矫正后不显著,促生长剂之间的差异极显著,试验批次间的差异不显著
作业
期货交易数据主要来源于某商品交易所,包括某水果期货上市以来的换手率、涨跌幅度、保证金、交易手续费、当日平仓手续费等,其它数据如灾害性天气状况等来源于网络资料。
换手率是期货表现热度的晴雨表,一般来讲,换手率越高,表明该产品越受到消费者青睐。请你查阅相关文献,研究本数据表,通过建立数学模型或统计分析方法,回答下列问题。
研究换手率的变化规律。
研究哪些因素对换手率是有影响的,哪些是没有影响的。
保证金、手续费、当日平仓、是否有灾害天气、是否消费旺季这几个影响因素之间是否有关联?
数据下载地址:
1.第一问
研究数据的变化规律我们主要从数据的周期、数据的趋势、数据的随机性、以及数据内部的传递性四个方面来研究
编写SAS代码:
1 | data a; |
得到时序图:
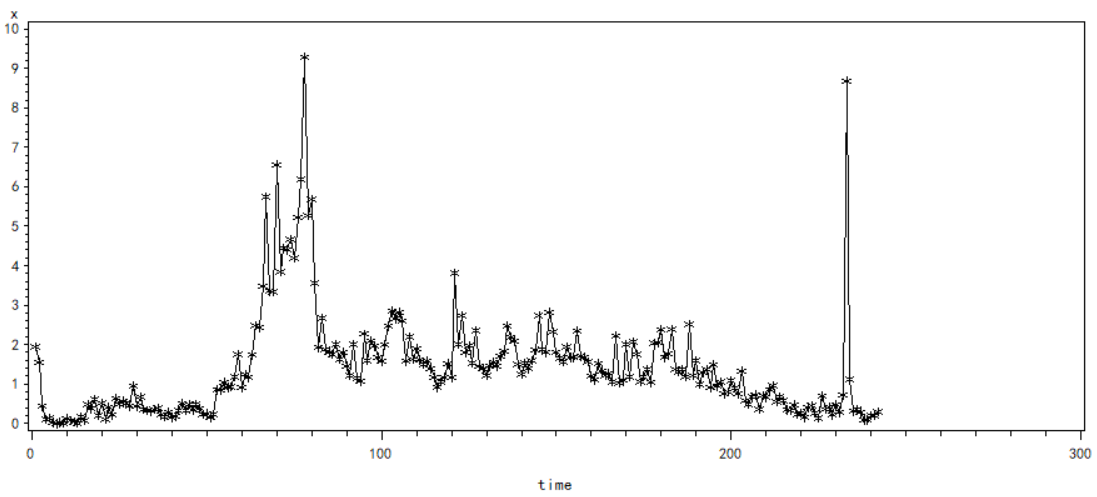
从图中我们可以看出数据大致可以判断为是不具有周期性波动的,且数据波动性较大,故初步判断该数据不是平稳的。然而由于根据时序图的判断严谨性不高,于是根据自相关图进行进一步的判断。
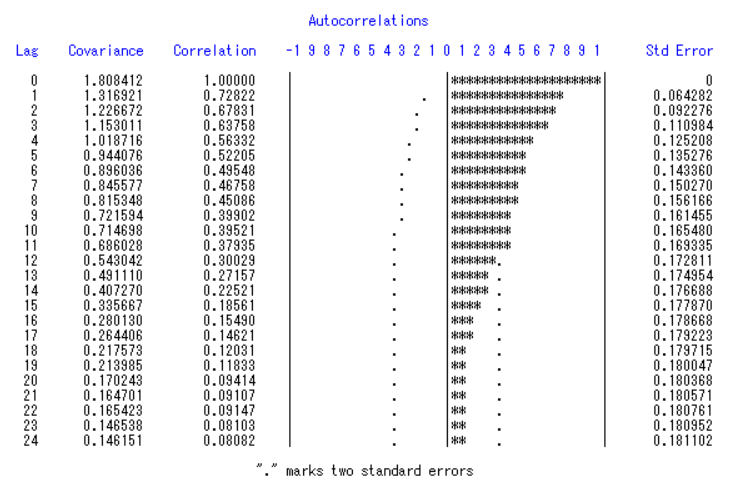
随着时间平移长度的增大,自相关系数的数值的变化并未呈周期性变化。从图片右半边的表示自相关系数的图也可以看出:自相关系数并不是是呈周期性波动。综合时序图的分析以及自相关图的分析,得到以下结论:该数据并不具有周期性且不平稳。
由于原始数据不具有平稳性我们需要对原始数据进行差分运算,故对原始数据进行一阶差分运算并且需要对运算后得出的数据进行平稳性检验,检验结果如下。
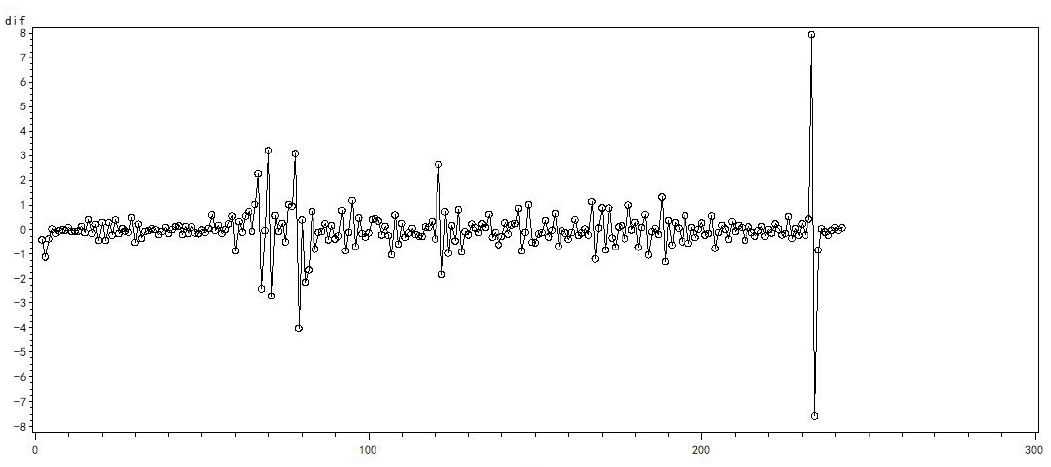
将数据一阶差分后按照月份做出来的时序图,从图中我们可以看出运算后数据大致可以判断为是在一条水平线上下波动,故初步判断该序列是平稳的。然而由于根据时序图的判断严谨性不高,于是根据自相关图进行进一步的判断。
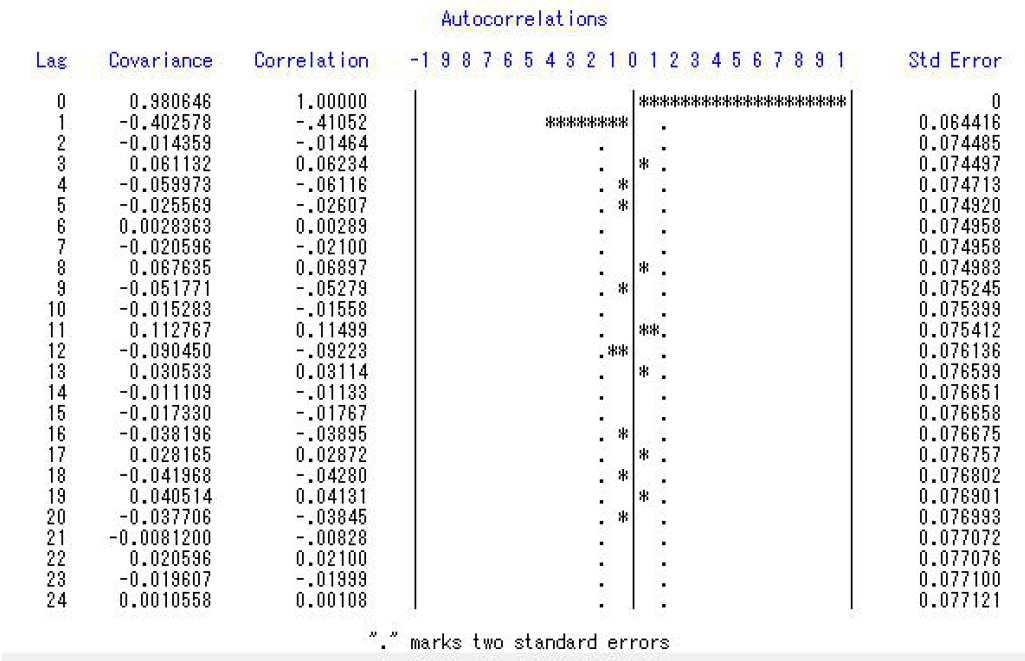
在时间平移长度较小时,自相关系数的数值较大,当时间平移长度扩大时,自相关系数的数值总体来说是在逐渐趋近于0,由此可以得出自相关系数具有拖尾性。从图片右半边的表示自相关系数的图也可以看出:自相关系数在0.0 这条线的左右波动。综合时序图的分析以及自相关图的分析,得到以下结论:该数据具有平稳性。由于通过一阶差分使得数据平稳,故该数据中具有线性趋势。
已知该序列在进行差分运算后是平稳的,要选择选择适当模型拟合该序列的发展还需要证明该序列在差分运算后是非白噪声的。白噪声检
验结果如下。
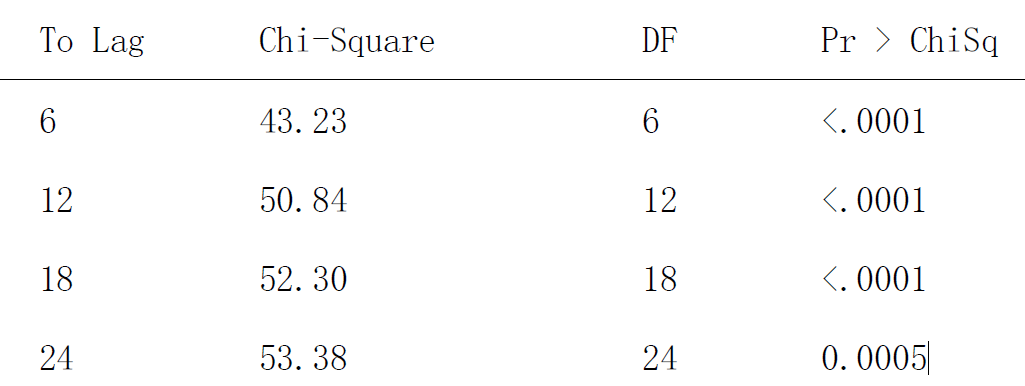
延迟6 期、延迟12 期、延迟18 期、延迟24 期的p值分别为<.0001、<.0001、<.0001、0.0005,都远小于0.05,故拒绝原假设,数据之间存在相关性,该数据在差分运算后是非白噪声的,故该数据不具有随机波动。
综合以上分析,得出以下结论:换手率的变化不具有周期性,具有线性趋势,数据内部具有相关性,不具有随机波动。
2.第二问
第二问要求对换手率有影响的因素,要研究的是变量和多个分类变量之间的关系,因此选择应用多组独立样本的H检验法进行研究。
SAS代码:
1 | data ex; |
最后得到如下结果:(按abcde排序)


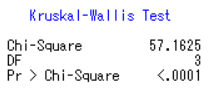
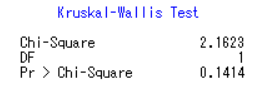
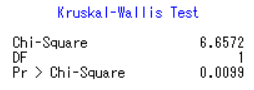
可以做成如下表格:
| 保证金因素 | 手续费因素 | 当日平仓因素 | 是否有灾害天气因素 | 是否消费旺季因素 | |
|---|---|---|---|---|---|
| Chi-Square | 65.6884 | 7.9437 | 29.3956 | 2.1623 | 6.6572 |
| DF | 4 | 2 | 2 | 1 | 1 |
| Pr > Chi-Square | <.0001 | 0.0188 | <.0001 | 0.1414 | 0.0099 |
可以看出保证金因素、手续费因素、当日平仓因素、是否消费旺季因素这四个因素的P值均小于0.05,落在拒绝域中,拒绝原假设,认为样本分布与换手率的样本分布不同,因此认为以上四个因素对换手率没有显著的影响;而是否有灾害天气因素的P值为0.1414大于0.05,接受原假设,认为认为样本分布与换手率的样本分布相同,因此认为是否有灾害天气因素对换手率有显著的影响。
3.第三问
第三问要求的是多个分类变量之间的关系,因此选用独立性检验来研究变量之间的关系。
SAS代码:
1 | data ex; |
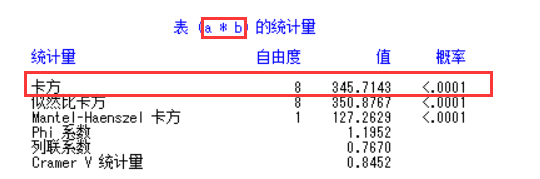
得到很多表,综合下来我们做出一张表:

保证金和手续费之间自由度为8,χ2 (Chi-Square value)=345.7143,且Prob值<0.0001<0.05,故落在拒绝域,接受备择假设,即保证金和手续费这两因素之间不是相互独立的,即保证金对手续费是有关系的,同理可知,保证金和当日平仓,保证金和是否消费旺季,手续费和当日平仓,手续费和是否消费旺季,当日平仓和是否消费旺季这些因素的Prob值均小于0.05,故落在拒绝域,接受备择假设,所以认为这些因素之间不是相互独立的,即保证金和对当日平仓,保证金对是否消费旺季,手续费对当日平仓,手续费对是否消费旺季都是有关系的,相反可以知道,保证金和是否有灾害天气,手续费和是否有灾害天气,当日平仓和是否有灾害天气,是否有灾害天气和是否消费旺季这些因素的Prob值均大于0.05,故落在接受域,接受原假设,所以认为这些因素之间是相互独立的,即保证金对是否有灾害天气,手续费对是否有灾害天气,当日平仓对是否有灾害天气,是否有灾害天气对是否消费旺季是没有影响的。
结语
溃疡好了,👴没理由再偷懒了,555555555


