数学建模-时间序列分析


阅读数: 次   

EverydayOneCat

海洋！img

知识点

1.笔记

image-20200712143326562

image-20200712143353945

image-20200712143413124

2.平稳性检验

时序图检验：根据平稳时间序列均值、方差为常数的性质，平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动，而且波动的范围有界、无明显趋势及周期特征。

自相关图检验：平稳序列通常具有短期相关性。该性质用自相关系数来描述就是随着延迟期数的增加，平稳序列的自相关系数会很快地衰减向零。

SAS代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
data a;
input  sha@@;
year=_n_;
dif=dif(sha);
cards;
97 130 156.5 135.2 137.7 180.5 205.2 190 188.6 196.7
180.3 210.8 196 223 238.2 263.5 292.6 317 335.4 327
321.9 353.5 397.8 436.8 465.7 476.7 462.6 460.8
501.8 501.5 489.5 542.3 512.2 559.8 542 567
;
run;
proc gplot;
plot sha*year=1 dif*year=2;
symbol1 v=circle i=join c=black;
symbol2 v=star i=join c=red;
proc arima data=a;
identify var=sha nlag=22;
run;

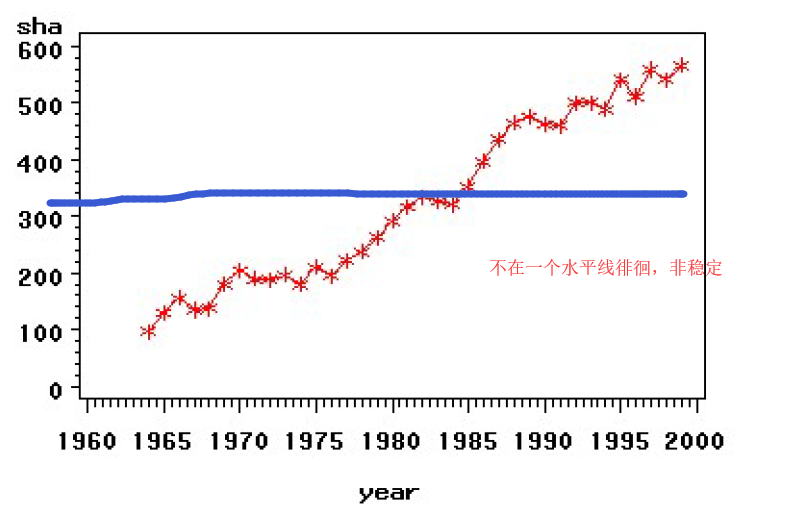
image-20200711103348004

image-20200711103401807

image-20200711103508683

此图没有明显周期，也没有明显趋势，基本可以判断是平稳的

image-20200711103540507

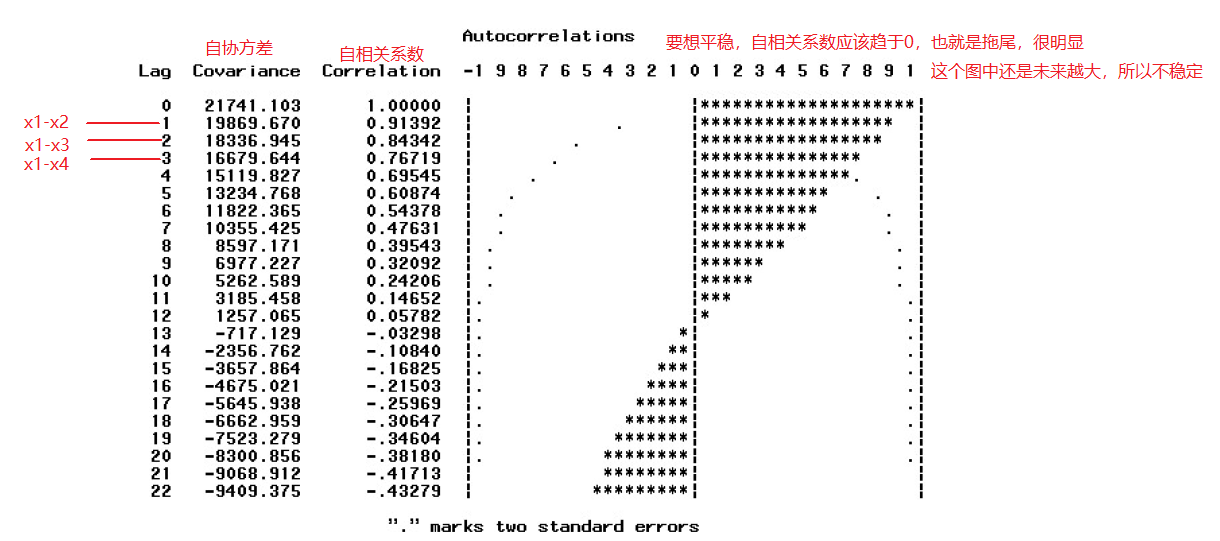
延迟了1步之后，他的相关系数稳定接近于0，说明这个序列具有短期相关性。

2.纯随机性检验

纯随机序列也称为白噪声序列，标准正态白噪声序列时序图

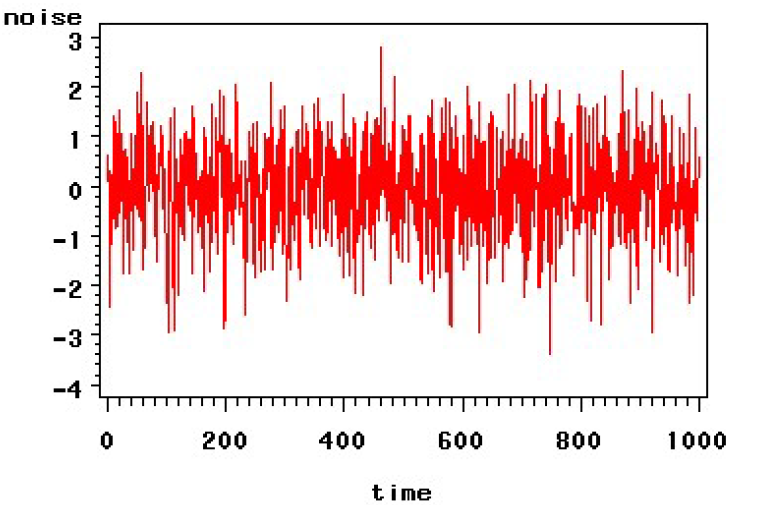
image-20200711104501189

1、首先判断是否平稳，平稳后才能判断是否纯随机

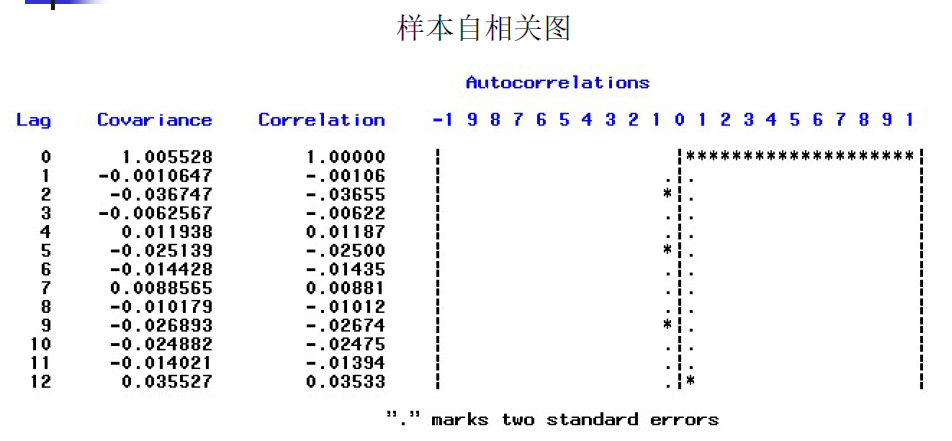
image-20200711104611321

2、白噪声检验

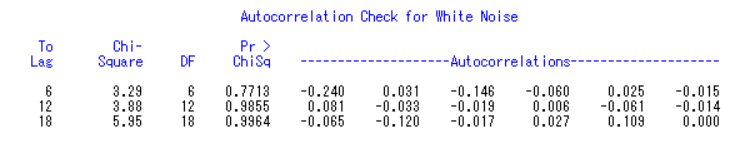
image-20200711105552462

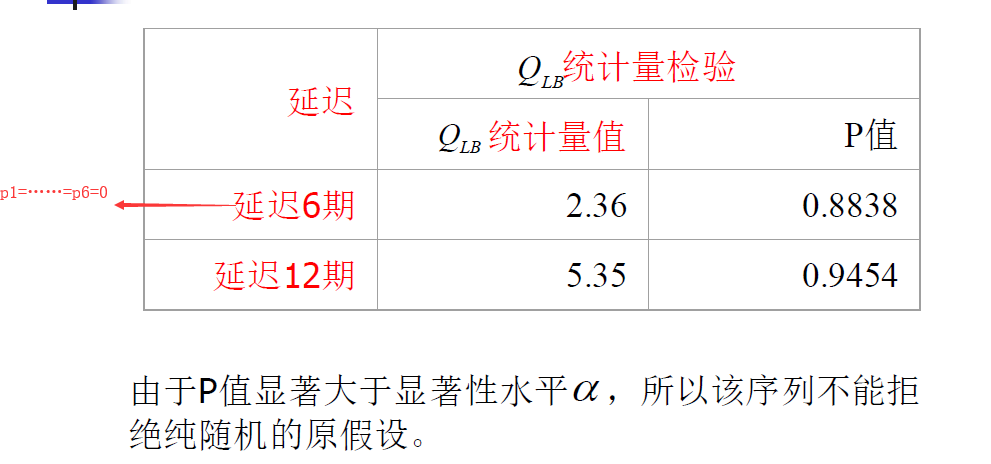
image-20200711104722474

3.平稳时间序列建模

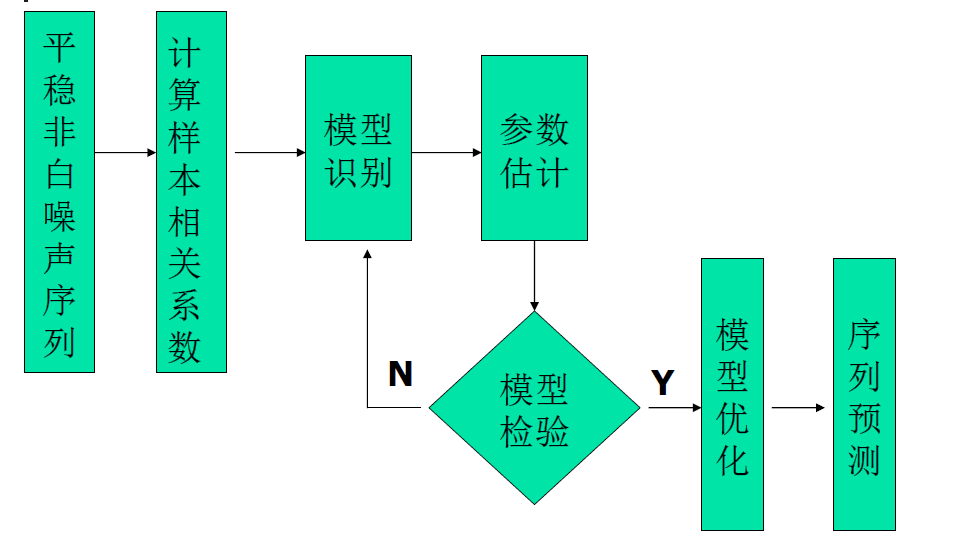
image-20200711134100075

选择合适的模型ARMA拟合1950年——1998年北京市城乡居民定期储蓄比例序列。

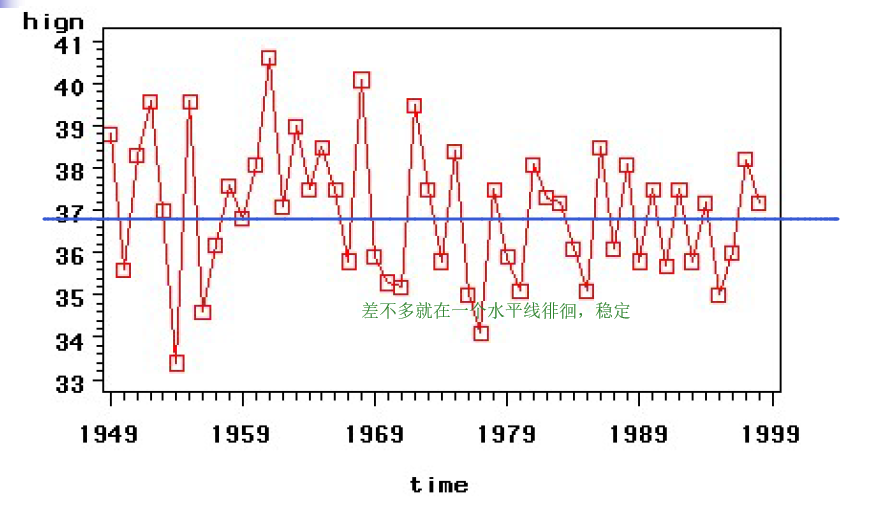
先进行平稳性检验：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
data a;
input year prop;
cards;
1950	83.5
1951	63.1
1952	71
1953	76.3
1954	70.5
1955	80.5
1956	73.6
1957	75.2
1958	69.1
1959	71.4
1960	73.6
1961	78.8
1962	84.4
1963	84.1
1964	83.3
1965	83.1
1966	81.6
1967	81.4
1968	84
1969	82.9
1970	83.5
1971	83.2
1972	82.2
1973	83.2
1974	83.5
1975	83.8
1976	84.5
1977	84.8
1978	83.9
1979	83.9
1980	81
1981	82.2
1982	82.7
1983	82.3
1984	80.9
1985	80.3
1986	81.3
1987	81.6
1988	83.4
1989	88.2
1990	89.6
1991	90.1
1992	88.2
1993	87
1994	87
1995	88.3
1996	87.8
1997	84.7
1998	80.2
;
proc gplot;
plot prop*year=1;
symbol1 v=diamond i=join c=red;
proc arima data=a;
identify var=prop nlag=22;
run;

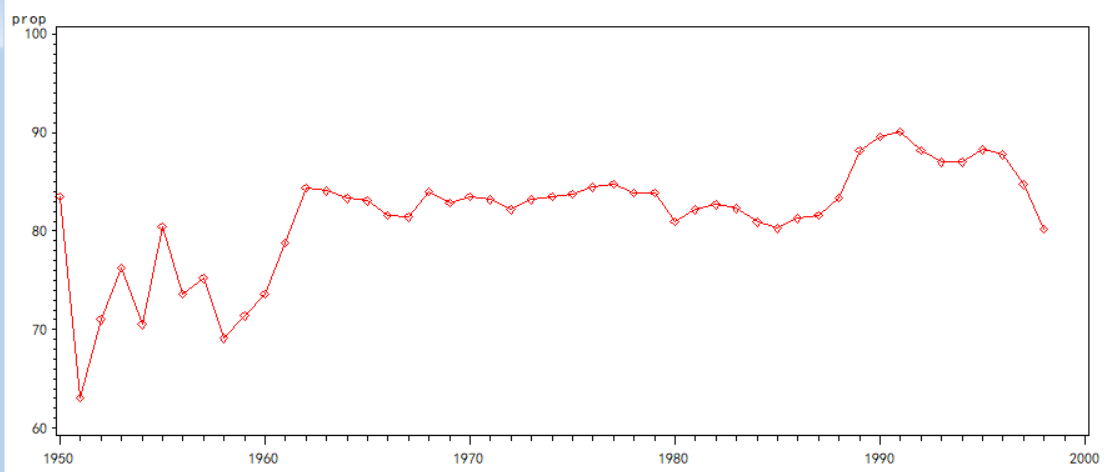
image-20200711114823754

image-20200711115054139

在0上下波动，说明此序列平稳。

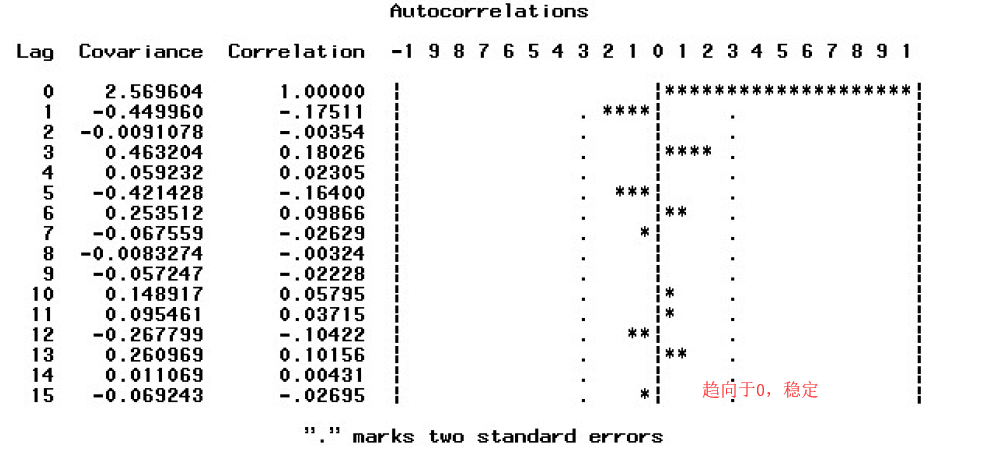
白噪声检验：

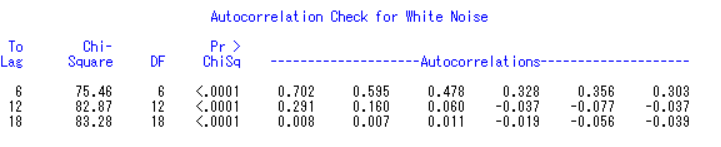
image-20200711115237015

拒绝原假设H0：p1=……=pi=0，说明序列之间有信息传递，是可以做一个ARMA模型的。

相对最优定阶方法：

为了尽量避免因个人经验不足导致的模型识别问题，SAS系统还提供了相对最优模型识别。只要在identify命令中加上一个可选命令minic，就可以获得一定范围内的最优模型定界。

修改代码：

1
identify var=prop nlag=22 minic p=(0:5)  q=(0:5);

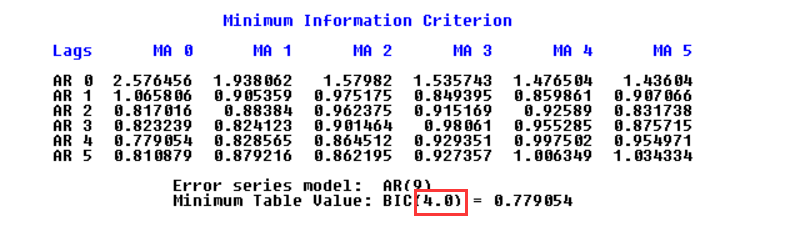
image-20200711130717961

说明p=4，q=0。推断出为AR模型

增加SAS代码：

1
estimate p=4 q=0;

image-20200711131311574

发现2,3,4没通过t检验。修改p=1

image-20200711132024022

可得出AR模型公式，类似于下图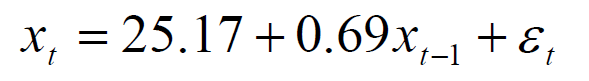image-20200711132257519

image-20200711132704326

残差需要接受白噪声检验。可以看出所有的都接受了原假设：残差序列为白噪声序列

image-20200711133054410

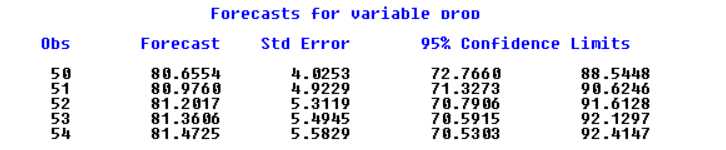
编写预测代码：

1
forecast id=year lead=5 out=out;

image-20200711133105822

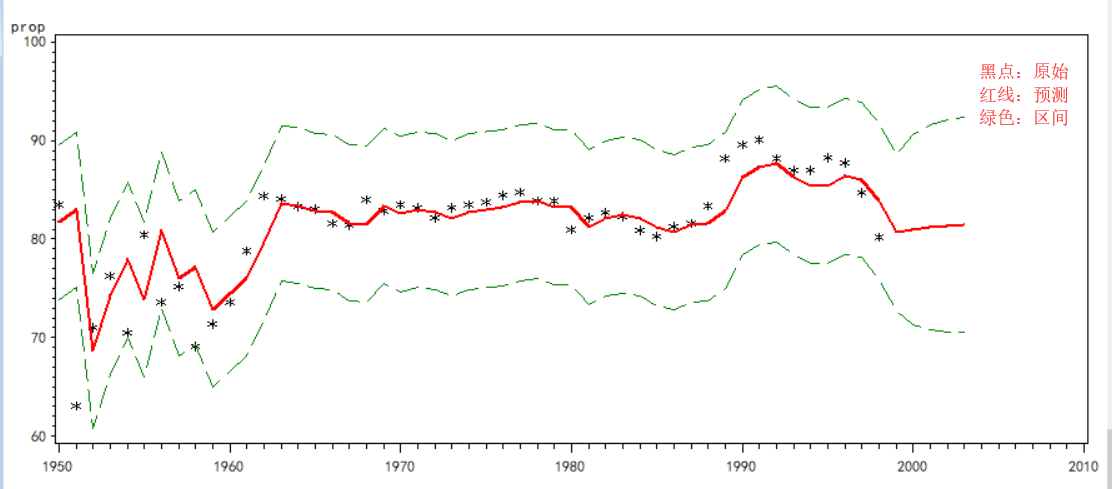
编写代码画图：

1
2
3
4
5
proc gplot data=out;
plot prop*year=2 forecast*year=3 l95*year=4 u95*year=4/overlay;
symbol2 v=star i=none c=black ;
symbol3 v=none i=join c=red w=2;
symbol4 v=none i=join c=green l=2 ;

image-20200711133317505

4.非平稳序列差分方式的选择

1、原序列时序图：

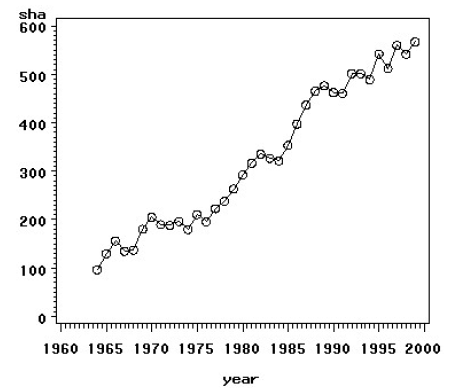
image-20200711155321160

差不多呈线性，我们使用一阶差分，差分后序列时序图：

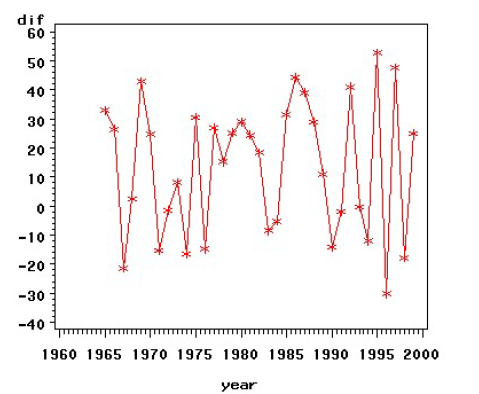
image-20200711155350282

2、原序列时序图：

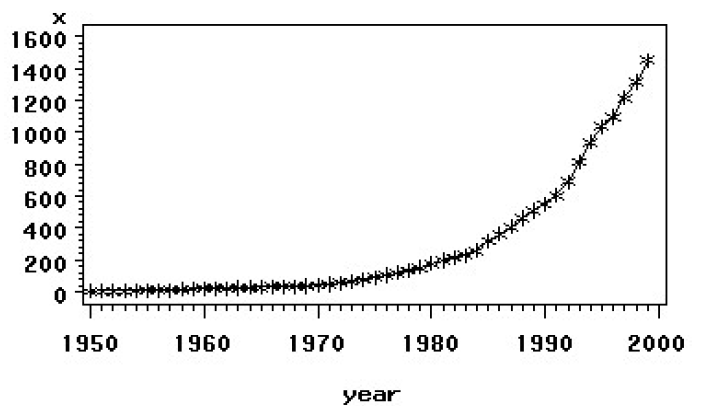
image-20200711155427275

曲线趋势，我们选择二阶差分：

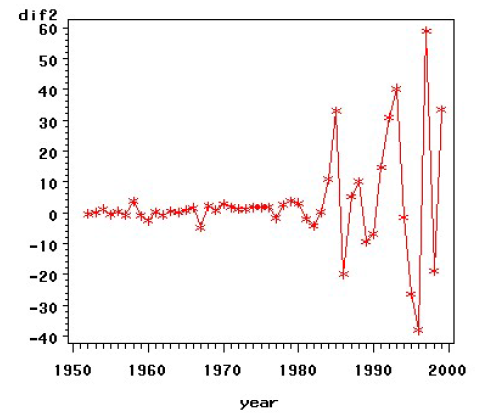
image-20200711155454965

3、原序列时序图：

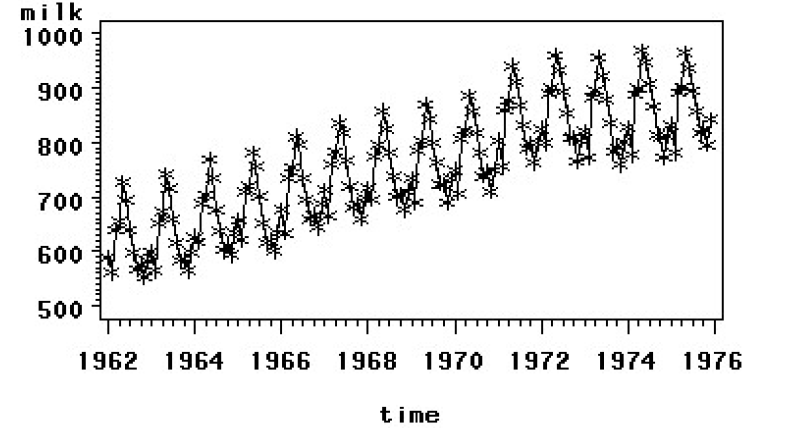
image-20200711155522220

差不多可以看出来是周期，我们通过SAS来观测周期时长

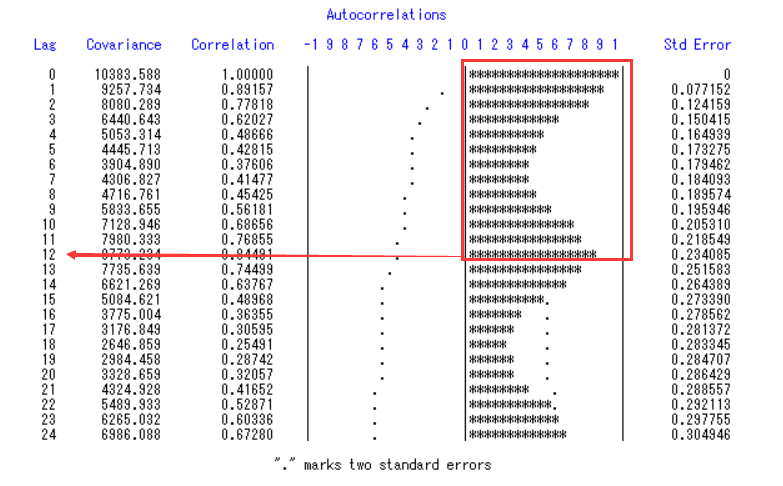
image-20200711155905801

可以看出周期为12，我们先做一阶差分，再做12步差分：

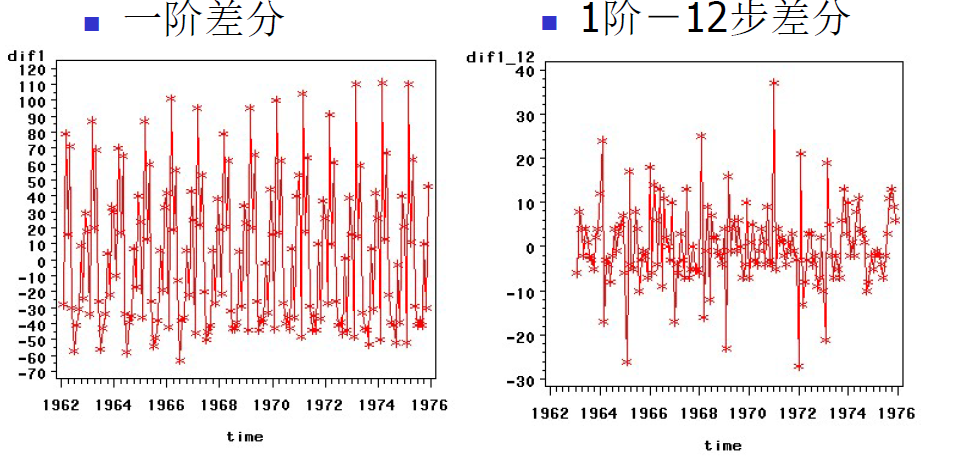
image-20200711160003127

5.ARIMA模型建模步骤

image-20200711170129178

对1952年——1988年中国农业实际国民收入指数序列建模

SAS代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
goptions vsize=7cm hsize=10cm;
data ex;
t=_n_;
input agric@@;
cards;
100     101.6   103.3   111.5   116.5   120.1   120.3   100.6   83.6    
84.7    88.7    98.9    111.9   122.9   131.9   134.2   131.6   132.2   
139.8   142     140.5   153.1   159.2   162.3   159.1   155.1   161.2   
171.5  168.4   180.4   201.6   218.7  247    253.7   261.4  273.2   279.4  
;
proc gplot;
plot agric*t=1;
symbol1 c=red i=join v=square;
proc arima;
identify var=agric(1) stationarity=(adf) nlag=18;
run;

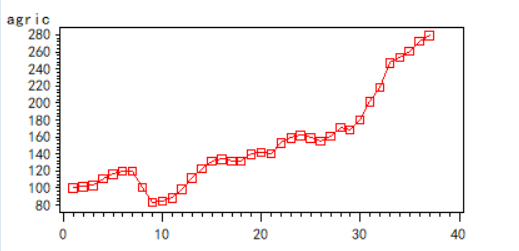
image-20200711170241403

有向上发展的趋势，我们需要进行差分

一步(一阶)差分：dif(xx)
二部差分：dif2(xx)
二阶差分：dif(dif(xx))

修改SAS代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
goptions vsize=7cm hsize=10cm;
data ex;
t=_n_;
input agric@@;
dif=dif(agric);
cards;
数据区
;
proc gplot;
plot dif*t=1;
symbol1 c=red i=join v=square;
proc arima;
identify var=dif stationarity=(adf) nlag=18;
run;

自相关系数图：

image-20200711170741965

可以看出差不多在0左右徘徊，我们再来看看时序图：

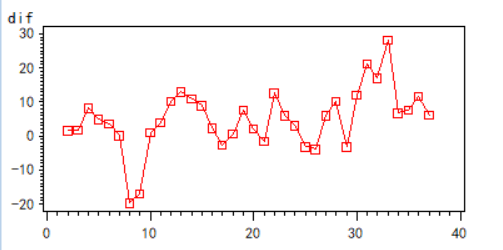
image-20200711170844259

综合以上，基本稳定。接着我们看一阶差分之后的白噪性检验：

image-20200711171054139

只要有一个里面比0.05小，就说明有信息传递，可以用时间序列拟合。

接下来做一阶差分的模型识别，修改SAS代码：

1
identify var=dif nlag=18 minic p=(0:5) q=(0:5);

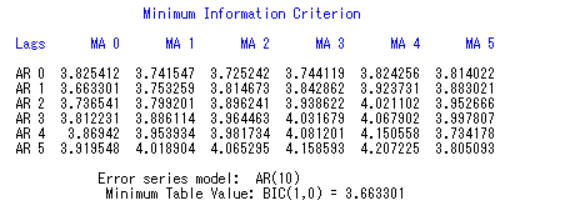
image-20200711171410473

得到p=1，q=0，模型为ARIMA(1,1,0)（中间参数是代表阶数）

模型的检验：

1
estimate p=1;

进行参数的检验：

image-20200711171635936

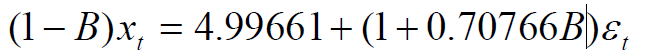
image-20200711173026422

对模型进行显著性检验，即对残差序列进行白噪声检验：

image-20200711171929770

都大于0.05，接受原假设，说明残差之间没有信息传递。

预测代码：

1
forecast lead=10 id=time interval=year out=out;

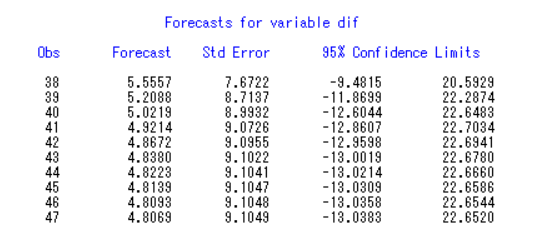
image-20200711172237321

这里预测的是一阶差分之后的数据量，我们如果想要看本来的数据，可以修改代码来使预测的数据导入原始序列：

一步(一阶)差分：xx(1)
二部差分：xx(2)
二阶差分：xx(1,1)
一阶12步差分：xx(1,12)

1
2
3
4
5
proc arima;
identify var=agric(1) nlag=18 minic p=(0:5) q=(0:5);/*agric(1)相当于dif*/
estimate p=1;
forecast lead=10 id=time interval=year out=out;
run;

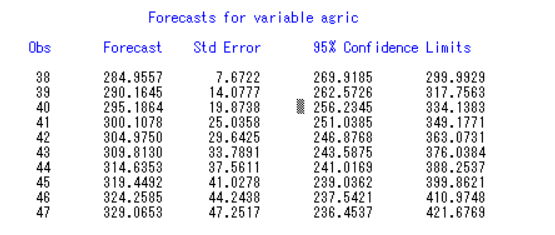
image-20200711172657286

6.疏系数模型

对1917年－1975年美国23岁妇女每万人生育率序列建模

初始SAS代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
goptions vsize=7cm hsize=10cm;
data a;
input year x@@;
dif=dif(x);
cards;
1917	183.1
1918	183.9
1919	163.1
1920	179.5
1921	181.4
1922	173.4
1923	167.6
1924	177.4
1925	171.7
1926	170.1
1927	163.7
1928	151.9
1929	145.4
1930	145
1931	138.9
1932	131.5
1933	125.7
1934	129.5
1935	129.6
1936	129.5
1937	132.2
1938	134.1
1939	132.1
1940	137.4
1941	148.1
1942	174.1
1943	174.7
1944	156.7
1945	143.3
1946	189.7
1947	212
1948	200.4
1949	201.8
1950	200.7
1951	215.6
1952	222.5
1953	231.5
1954	237.9
1955	244
1956	259.4
1957	268.8
1958	264.3
1959	264.5
1960	268.1
1961	264
1962	252.8
1963	240
1964	229.1
1965	204.8
1966	193.3
1967	179
1968	178.1
1969	181.1
1970	165.6
1971	159.8
1972	136.1
1973	126.3
1974	123.3
1975	118.5
;
proc gplot;
plot x*year dif*year;
symbol c=black i=join v=square;
proc arima;
identify var=x nlag=22;
run;

image-20200711233116659

发现初始序列并不稳定，我们做一阶差分。

1
identify var=x(1);

image-20200711233206614

自相关系数趋向于0，说明一阶差分后稳定了

接着我们需要确定模型

1
identify var=x(1) nlag=22 minic p=(0:5) q=(0:5);

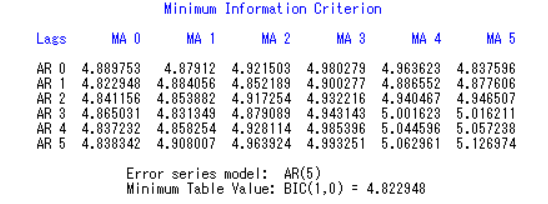
image-20200711233552697

这里最好选择p=1，但是我们为了研究疏系数模型，我们取次小的p=4来研究

参数分析：

1
estimate p=4;

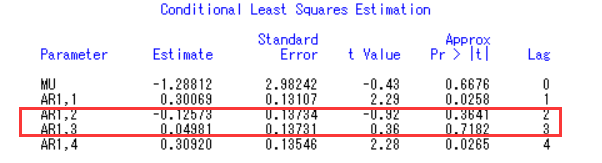
image-20200711233746204

常数，AR2，AR3接受了原假设，需要去掉，修改代码：

1
estimate p=(1 4) noint;

image-20200711233856197

残差检验：所有的都要大于0.05

image-20200711233924300

接着就可以做预测了：

1
2
3
4
5
6
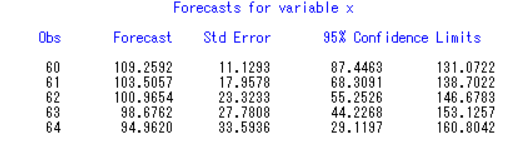
7
forecast lead=5 id=year out=out;
proc gplot data=out;
plot x*year=1 forecast*year=2 l95*year=3 u95*year=3/overlay;
symbol1 c=black i=none v=star;
symbol2 c=red i=join v=none;
symbol3 c=green i=join v=none;
run;

image-20200711234321344

image-20200711234330329

7.简单季节模型

拟合1962——1991年德国工人季度失业率序列

初始SAS代码：(首先这个肯定不平稳，我们直接跳到一阶差分)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
goptions vsize=7cm hsize=10cm;
data a;
input x@@;
dif1=dif(x);
time=1962+_n_;
cards;
1.1	0.5	0.4	0.7	1.6	0.6	0.5	0.7
1.3	0.6	0.5	0.7	1.2	0.5	0.4	0.6
0.9	0.5	0.5	1.1	2.9	2.1	1.7	2
2.7	1.3	0.9	1	1.6	0.6	0.5	0.7
1.1	0.5	0.5	0.6	1.2	0.7	0.7	1
1.5	1	0.9	1.1	1.5	1	1	1.6
2.6	2.1	2.3	3.6	5	4.5	4.5	4.9
5.7	4.3	4	4.4	5.2	4.3	4.2	4.5
5.2	4.1	3.9	4.1	4.8	3.5	3.4	3.5
4.2	3.4	3.6	4.3	5.5	4.8	5.4	6.5
8	7	7.4	8.5	10.1	8.9	8.8	9
10	8.7	8.8	8.9	10.4	8.9	8.9	9
10.2	8.6	8.4	8.4	9.9	8.5	8.6	8.7
9.8	8.6	8.4	8.2	8.8	7.6	7.5	7.6
8.1	7.1	6.9	6.6	6.8	6	6.2	6.2
;
proc gplot;
plot x*time dif1*time;
symbol c=black i=join v=star;
proc arima;
identify var=x(1);
run;

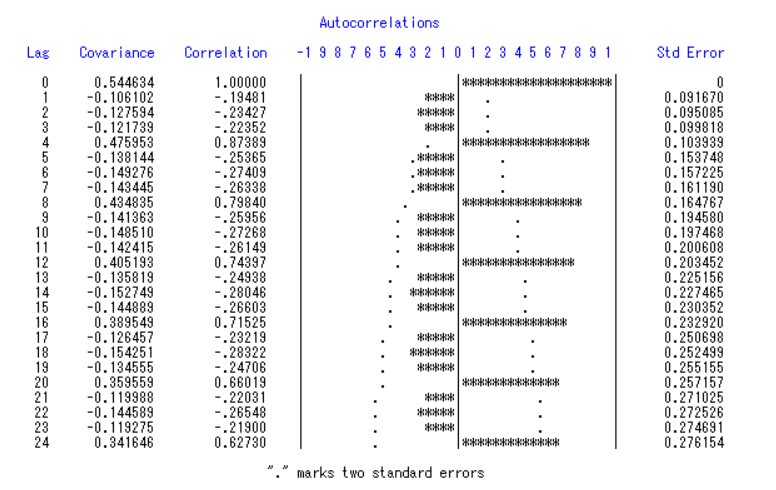
image-20200712103719265

可以看出，一阶差分之后周期性还是很明显的。我们可以发现周期大概是四，因此我们在此基础上再来四步差分。修改SAS代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
goptions vsize=7cm hsize=10cm;
data a;
input x@@;
dif1_4=dif4(dif(x));
time=1962+_n_;
cards;
数据区
;
proc gplot;
plot x*time dif1_4*time;
symbol c=black i=join v=star;
proc arima;
identify var=x(1 4);
run;

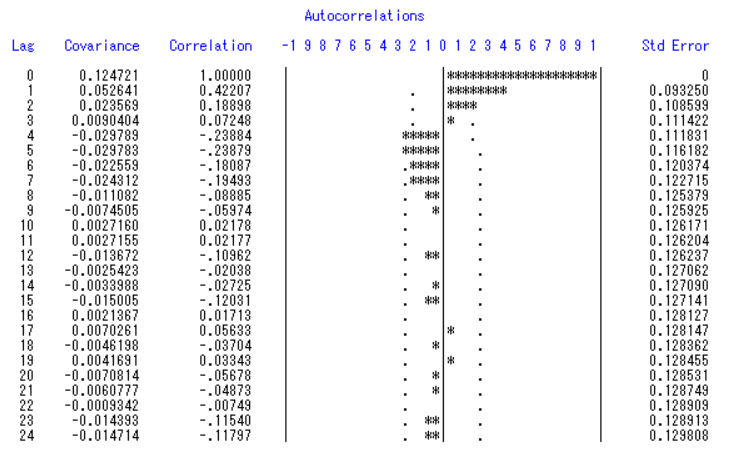
image-20200712104015913

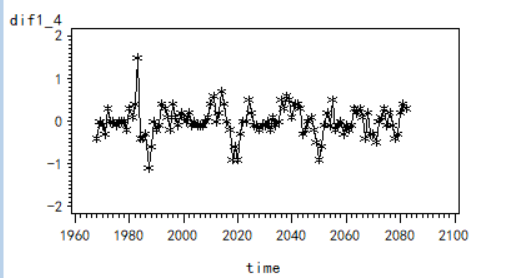
image-20200712104028956

综合自相关系数表和时序图可以看出此时时间序列平稳了，接着我们还需要看白噪声检验：

image-20200712104126688

都小于0.05，说明一阶四步差分之后的序列可以做时间序列的模型。

接着我们要预测模型（此步上面都有，不再赘述），试出来是p=4，再进行参数检验，最后p=(1 4) noint，定阶模型为ARIMA((1,4),(1,4),0)。

最后看残差的白噪声检验，通过了就可以做预测了，附上SAS代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
goptions vsize=7cm hsize=10cm;
data a;
input x@@;
dif1=dif(x);
dif1_4=dif4(dif(x));
time=1962+_n_;
cards;
数据区
;
proc gplot;
plot x*time dif1_4*time;
symbol c=black i=join v=star;
proc arima;
identify var=x(1 4);
estimate p=(1 4) noint;
forecast lead=5 id=time out=out;
proc gplot data=out;
plot x*time=1 forecast*time=2 /overlay;
symbol1 c=black i=none v=star;
symbol2 c=red i=join v=none;
run;

image-20200712104736968

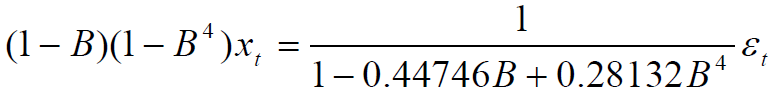
参数估计：image-20200712104749329

8.乘积季节模型

拟合1948——1981年美国女性月度失业率序列

初始SAS代码：(原始序列不稳定确定过程略过，直接先进行一阶差分)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
data a;
input x@@;
dif1_12=dif12(dif(x));
time=_n_;
cards;
446	650	592	561	491	592	604	635	580
510	553	554	628	708	629	724	820	865
1007	1025	955	889	965	878	1103	1092	978
823	827	928	838	720	756	658	838	684
779	754	794	681	658	644	622	588	720
670	746	616	646	678	552	560	578	514
541	576	522	530	564	442	520	484	538
454	404	424	432	458	556	506	633	708
1013	1031	1101	1061	1048	1005	987	1006	1075
854	1008	777	982	894	795	799	781	776
761	839	842	811	843	753	848	756	848
828	857	838	986	847	801	739	865	767
941	846	768	709	798	831	833	798	806
771	951	799	1156	1332	1276	1373	1325	1326
1314	1343	1225	1133	1075	1023	1266	1237	1180
1046	1010	1010	1046	985	971	1037	1026	947
1097	1018	1054	978	955	1067	1132	1092	1019
1110	1262	1174	1391	1533	1479	1411	1370	1486
1451	1309	1316	1319	1233	1113	1363	1245	1205
1084	1048	1131	1138	1271	1244	1139	1205	1030
1300	1319	1198	1147	1140	1216	1200	1271	1254
1203	1272	1073	1375	1400	1322	1214	1096	1198
1132	1193	1163	1120	1164	966	1154	1306	1123
1033	940	1151	1013	1105	1011	963	1040	838
1012	963	888	840	880	939	868	1001	956
966	896	843	1180	1103	1044	972	897	1103
1056	1055	1287	1231	1076	929	1105	1127	988
903	845	1020	994	1036	1050	977	956	818
1031	1061	964	967	867	1058	987	1119	1202
1097	994	840	1086	1238	1264	1171	1206	1303
1393	1463	1601	1495	1561	1404	1705	1739	1667
1599	1516	1625	1629	1809	1831	1665	1659	1457
1707	1607	1616	1522	1585	1657	1717	1789	1814
1698	1481	1330	1646	1596	1496	1386	1302	1524
1547	1632	1668	1421	1475	1396	1706	1715	1586
1477	1500	1648	1745	1856	2067	1856	2104	2061
2809	2783	2748	2642	2628	2714	2699	2776	2795
2673	2558	2394	2784	2751	2521	2372	2202	2469
2686	2815	2831	2661	2590	2383	2670	2771	2628
2381	2224	2556	2512	2690	2726	2493	2544	2232
2494	2315	2217	2100	2116	2319	2491	2432	2470
2191	2241	2117	2370	2392	2255	2077	2047	2255
2233	2539	2394	2341	2231	2171	2487	2449	2300
2387	2474	2667	2791	2904	2737	2849	2723	2613
2950	2825	2717	2593	2703	2836	2938	2975	3064
3092	3063	2991						
;
proc gplot;
plot x*time dif1_12*time;
symbol c=black i=join v=none;
proc arima;
identify var=x(1);
run;

image-20200712111526775

可以看出周期差不多是12，因此在进行12步差分

1
identify var=x(1,12);

先进行差分平稳：

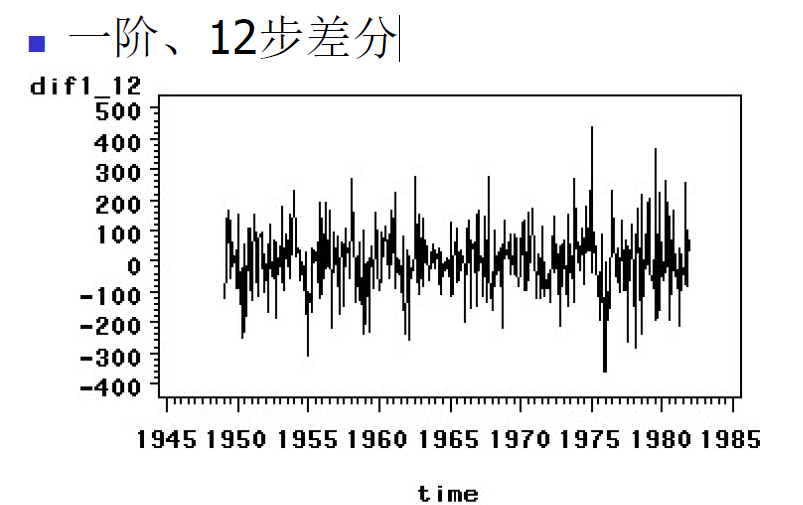
image-20200712110248454

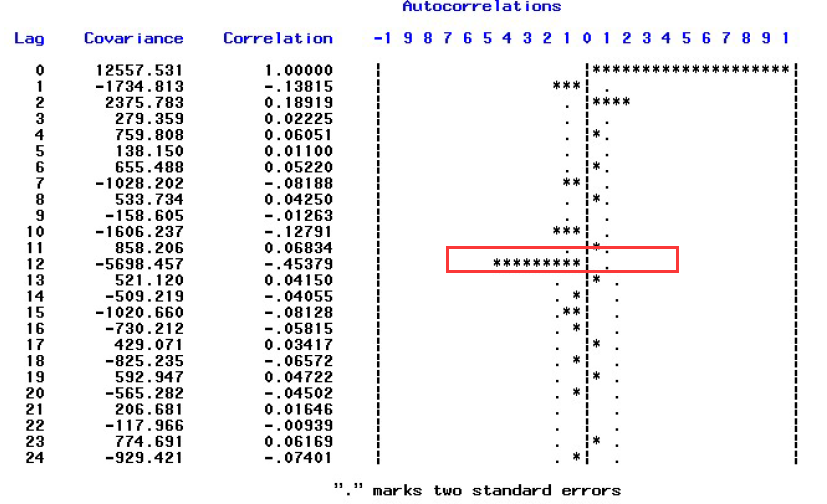
得到的自相关系数图：

image-20200712110321230

偏自相关系数图：

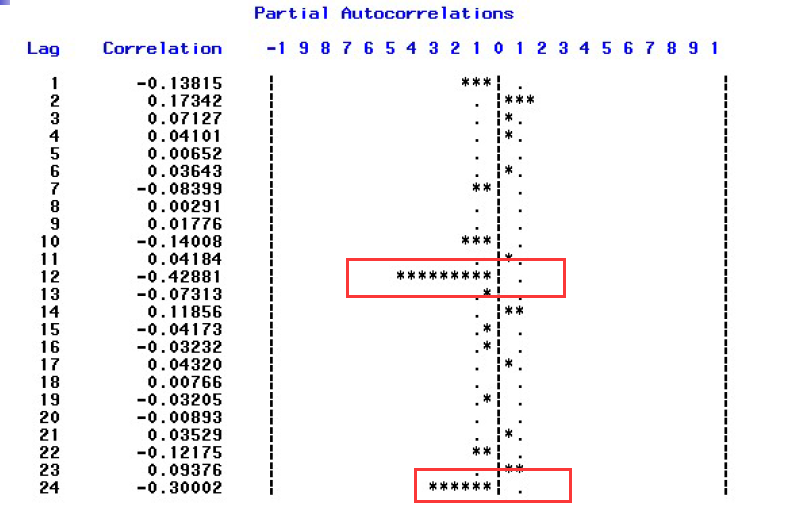
image-20200712110452182

从上面这两张图差不多可以看出进行了差分后并没有完全平稳，接着我们制定模型，中间的参数检验逐步把p(AR)和q(MA)不符合的去掉，最后得到p=0,q=1 noint;

再看残差白噪声检验：

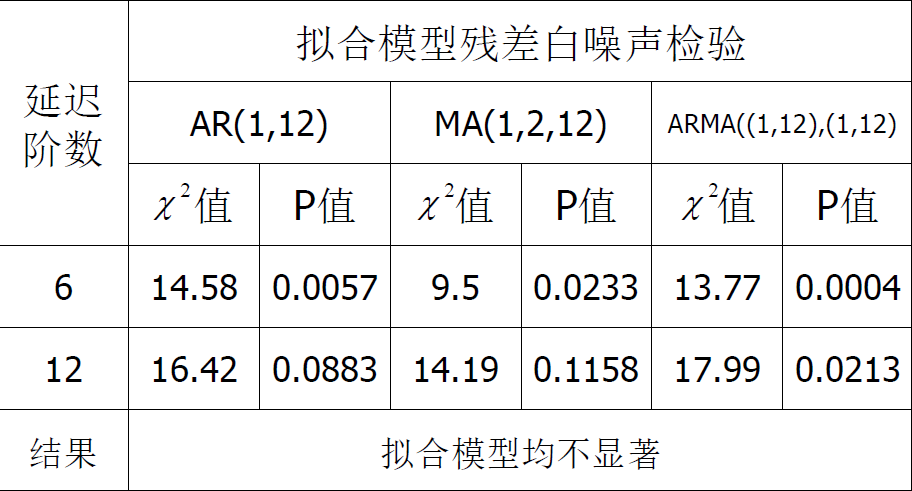
image-20200712110725586

好几个小于0.05，说明残差直接有信息传递，这时候我们发现简单季节模型并不适用，我们考虑使用乘积季节模型

image-20200712113718281

最终调试出来的代码：

1
estimate p=1 q=(1)(12) noint;

image-20200712113954779

参数检验通过

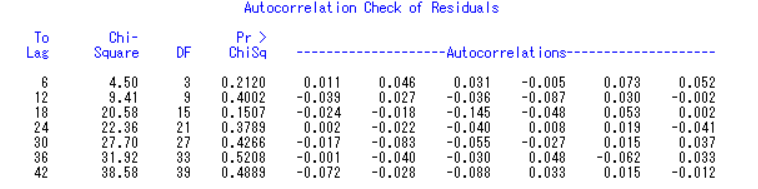
image-20200712114017028

残差白噪声检验也通过了。

模型定阶：image-20200712114300170

image-20200712115452313

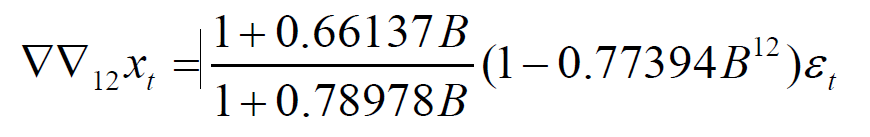
image-20200712115354214

作业

1.平稳时间序列

现有201个连续的生产纪录，如下

81.9 89.4 79.0 81.4 84.8 85.9 88.0 80.3 82.6
83.5 80.2 85.2 87.2 83.5 84.3 82.9 84.7 82.9
81.5 83.4 87.7 81.8 79.6 85.8 77.9 89.7 85.4
86.3 80.7 83.8 90.5 84.5 82.4 86.7 83.0 81.8
89.3 79.3 82.7 88.0 79.6 87.8 83.6 79.5 83.3
88.4 86.6 84.6 79.7 86.0 84.2 83.0 84.8 83.6
81.8 85.9 88.2 83.5 87.2 83.7 87.3 83.0 90.5
80.7 83.1 86.5 90.0 77.5 84.7 84.6 87.2 80.5
86.1 82.6 85.4 84.7 82.8 81.9 83.6 86.8 84.0
84.2 82.8 83.0 82.0 84.7 84.4 88.9 82.4 83.0
85.0 82.2 81.6 86.2 85.4 82.1 81.4 85.0 85.8
84.2 83.5 86.5 85.0 80.4 85.7 86.7 86.7 82.3
86.4 82.5 82.0 79.5 86.7 80.5 91.7 81.6 83.9
85.6 84.8 78.4 89.9 85.0 86.2 83.0 85.4 84.4
84.5 86.2 85.6 83.2 85.7 83.5 80.1 82.2 88.6
82.0 85.0 85.2 85.3 84.3 82.3 89.7 84.8 83.1
80.6 87.4 86.8 83.5 86.2 84.1 82.3 84.8 86.6
83.5 78.1 88.8 81.9 83.3 80.0 87.2 83.3 86.6
79.5 84.1 82.2 90.8 86.5 79.7 81.0 87.2 81.6
84.4 84.4 82.2 88.9 80.9 85.1 87.1 84.0 76.5
82.7 85.1 83.3 90.4 81.0 80.3 79.8 89.0 83.7
80.9 87.3 81.1 85.6 86.6 80.0 86.6 83.3 83.1
82.3 86.7 80.2
（1）判断该序列的平稳性
（2）如果该序列平稳且非白噪声。选择适当模型拟合该序列的发展
（3）写出拟合模型，预测该序列后5年的95%预测的置信区间。

1、首先我们进行平稳性和非白噪声检验并初步确立模型，编写对应的SAS代码

1
2
3
4
5
6
7
8
9
10
11
12
13
data ex;
input prop@@;
year=_n_;
dif=dif(prop);
cards;
/*数据区*/
;
proc gplot;
plot prop*year=1;
symbol1 v=diamond i=join c=red;
proc arima data=ex;
identify var=prop nlag=22 minic p=(0:5)  q=(0:5);
run;

时序图：

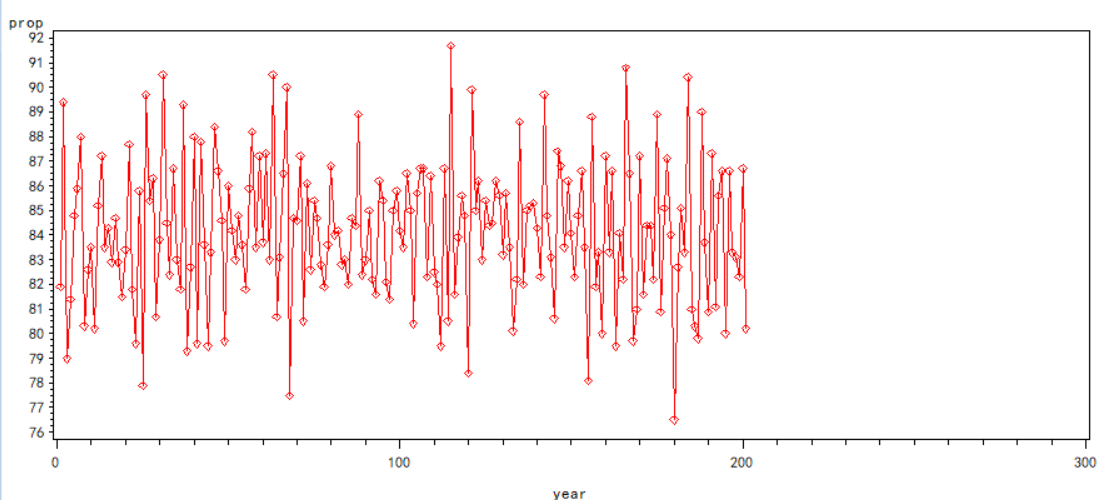
image-20200711140722673

已知时间序列为平稳序列的条件如下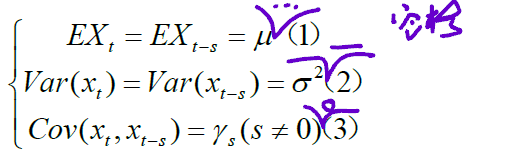：image-20200711140843032

观察时间序列图可知，序列基本上在一条水平线上下波动，可知该组数据的均值基本不变，为固定值，满足条件（1）；序列的波动性较小可判断其方差存在且可能为常数，满足条件（2）。因此，从该时间序列图我们猜测数据可能为平稳序列。接着，通过自相关图中自相关系数的变化进一步判断。

自相关系数图：

image-20200711140738779

由自相关系数图可知，当跨越步数p为0 时，自相关系数为1，此时自相关系数最大。随着跨越步数的逐渐增大，自相关系数的绝对值越小。跨越步数越大，自相关系数的绝对值越接近于0，具有拖尾的性质。可见，该序列是平稳序列。

2、在序列为平稳序列的基础上，我们对该序列进行白噪声检验

白噪声检验表：

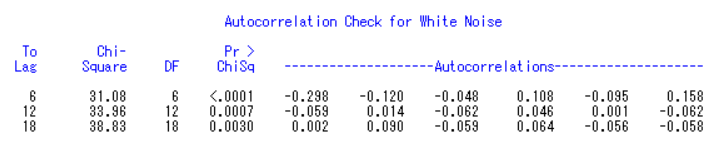
image-20200711141041020

image-20200711141103666

说明存在序列相关性，不满足纯随机序列 ，可以用时间序列拟合

3、调用SAS,对生产量进行minic 识别，指定p 和q 的最小值都为0，最大值都为6，得到BIC 信息指数如下：

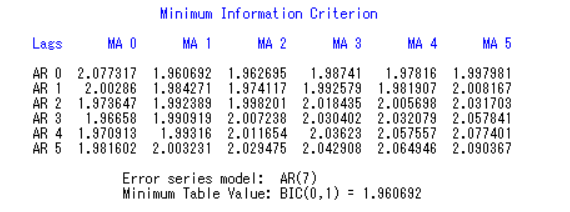
image-20200711141244059

暂时确定p=0，q=1，该序列为MA模型。

4、使用条件最小二乘估计进行参数估计，参数估计值如下表：

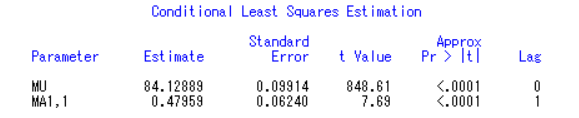
image-20200711141622621

其中，第一列为估计的参数名称，第二列是参数的估计值，第三列是参数估计值的标准误，第四列是参数显著性检验的 t 值，第五列为显著性检验的概率值 P。

可以发现 MU 和 MA1 ,1 的 P 值均小于 0.05 ，通过了 t 检验，得出移动平均系数多项式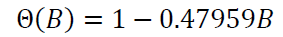：image-20200711141813927

根据移动平均模型的定义：𝑥𝑡=Θ(𝐵)𝜀𝑡，又可以推出 时间序列模型：𝑥𝑡=84.12889+(1−0.47959𝐵)𝜀𝑡

5、接着对模型进行显著性检验，即对残差序列进行白噪声检验，得到的残差序列检验表如下：

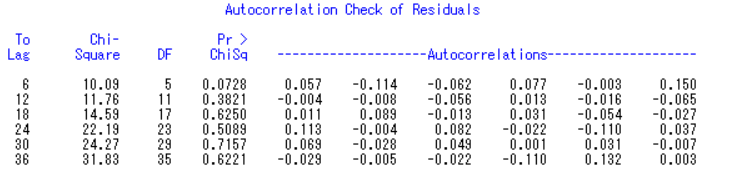
image-20200711142223055

可以看出，对 36 期的残差序列进行显著性检验后，其 P 值均大于 0.05 ，接受了原假设，服从白噪声序列，说明拟合模型能够提取观察值序列中几乎所有的样本相关信能够提取观察值序列中几乎所有的样本相关信息息。。

6、预测该序列后5 年的 95% 预测的置信区间 ，结果如表：

image-20200711142320478

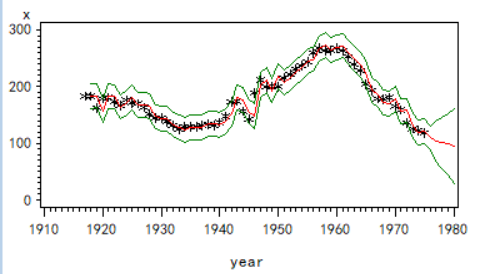
通过预测数据绘制除原数据与预测数据的拟合曲线如下图：

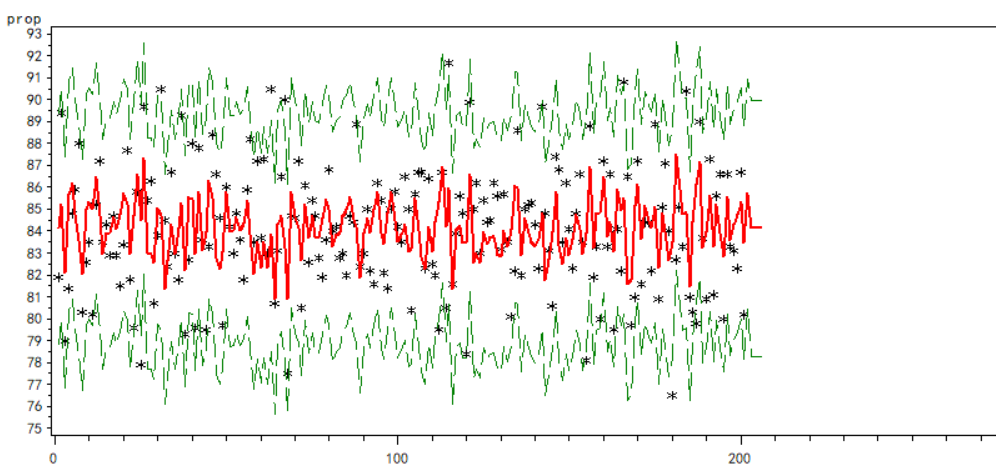
image-20200711142355048

由预测曲线图可以看出，大部分原数据在预测曲线上，预测趋势与原数据走势基本相似。
不在预测曲线上的数据几乎全部落在95%的预测曲线内，预测效果较好。

2.非平稳时间序列

习题：某城市连续14年的月度婴儿出生率数据如下
26.663 23.598 26.931 24.740 25.806 24.364 24.477 23.901
23.175 23.227 21.672 21.870 21.439 21.089 23.709 21.669
21.752 20.761 23.479 23.824 23.105 23.110 21.759 22.073
21.937 20.035 23.590 21.672 22.222 22.123 23.950 23.504
22.238 23.142 21.059 21.573 21.548 20.000 22.424 20.615
21.761 22.874 24.104 23.748 23.262 22.907 21.519 22.025
22.604 20.894 24.677 23.673 25.320 23.583 24.671 24.454
24.122 24.252 22.084 22.991 23.287 23.049 25.076 24.037
24.430 24.667 26.451 25.618 25.014 25.110 22.964 23.981
23.798 22.270 24.775 22.646 23.988 24.737 26.276 25.816
25.210 25.199 23.162 24.707 24.364 22.644 25.565 24.062
25.431 24.635 27.009 26.606 26.268 26.462 25.246 25.180
24.657 23.304 26.982 26.199 27.210 26.122 26.706 26.878
26.152 26.379 24.712 25.688 24.990 24.239 26.721 23.475
24.767 26.219 28.361 28.599 27.914 27.784 25.693 26.881
26.217 24.218 27.914 26.975 28.527 27.139 28.982 28.169
28.056 29.136 26.291 26.987 26.589 24.848 27.543 26.896
28.878 27.390 28.065 28.141 29.048 28.484 26.634 27.735
27.132 24.924 28.963 26.589 27.931 28.009 29.229 28.759
28.405 27.945 25.912 26.619 26.076 25.286 27.660 25.951
26.398 25.565 28.865 30.000 29.261 29.012 26.992 27.897

（1）选择适当的模型拟合该序列的发展
（2）使用该拟合模型预测下一年度该城市月度婴儿出生率

1、首先我们先绘制原本数据的时间序列图，初始SAS代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
goptions vsize=7cm hsize=10cm;
data a;
input x@@;
time=_n_;
cards;
26.663	23.598	26.931	24.740	25.806	24.364	24.477	23.901
23.175	23.227	21.672	21.870	21.439	21.089	23.709	21.669
21.752	20.761	23.479	23.824	23.105	23.110	21.759	22.073
21.937	20.035	23.590	21.672	22.222	22.123	23.950	23.504
22.238	23.142	21.059	21.573	21.548	20.000	22.424	20.615
21.761	22.874	24.104	23.748	23.262	22.907	21.519	22.025
22.604	20.894	24.677	23.673	25.320	23.583	24.671	24.454
24.122	24.252	22.084	22.991	23.287	23.049	25.076	24.037
24.430	24.667	26.451	25.618	25.014	25.110	22.964	23.981
23.798	22.270	24.775	22.646	23.988	24.737	26.276	25.816
25.210	25.199	23.162	24.707	24.364	22.644	25.565	24.062
25.431	24.635	27.009	26.606	26.268	26.462	25.246	25.180
24.657	23.304	26.982	26.199	27.210	26.122	26.706	26.878
26.152	26.379	24.712	25.688	24.990	24.239	26.721	23.475
24.767	26.219	28.361	28.599	27.914	27.784	25.693	26.881
26.217	24.218	27.914	26.975	28.527	27.139	28.982	28.169
28.056	29.136	26.291	26.987	26.589	24.848	27.543	26.896
28.878	27.390	28.065	28.141	29.048	28.484	26.634	27.735
27.132	24.924	28.963	26.589	27.931	28.009	29.229	28.759
28.405	27.945	25.912	26.619	26.076	25.286	27.660	25.951
26.398	25.565	28.865	30.000	29.261	29.012	26.992	27.897
;
proc gplot;
plot x*time;
symbol c=black i=join v=star;
proc arima;
identify var=x;
run;

时间序列图：

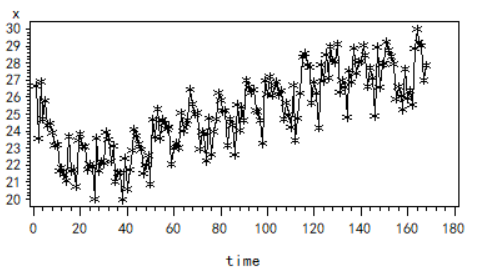
image-20200712115950952

自相关系数：

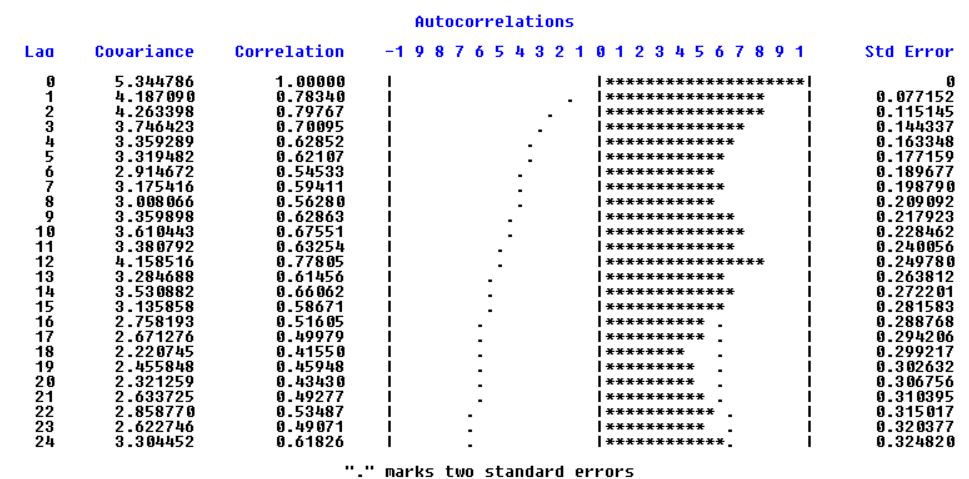
image-20200712120025799

可以看出序列非平稳，接着我们对序列进行差分处理，希望消除其周期性和趋势性。

2、一阶差分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
goptions vsize=7cm hsize=10cm;
data a;
input x@@;
dif=dif(x);
time=_n_;
cards;
数据区
;
proc gplot;
plot x*time dif*time;
symbol c=black i=join v=star;
proc arima;
identify var=x(1);
run;

时间序列图：
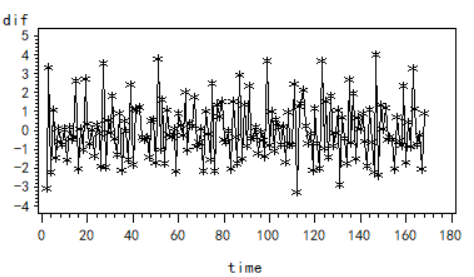
image-20200712120558943

image-20200712120537754

可以看出数据仍存在明显的周期性。估计其周期大致为12，接着用逐步差分消除周期性。

3、十二步差分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
goptions vsize=7cm hsize=10cm;
data a;
input x@@;
dif1_12=dif12(dif(x));
time=_n_;
cards;
数据区
;
proc gplot;
plot x*time dif1_12*time;
symbol c=black i=join v=star;
proc arima;
identify var=x(1,12);
run;

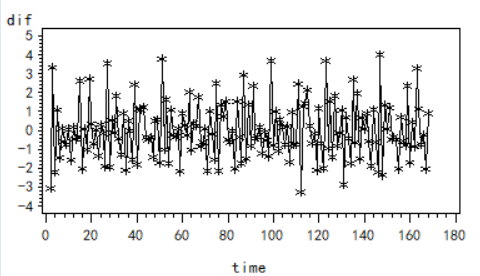
image-20200712120903657

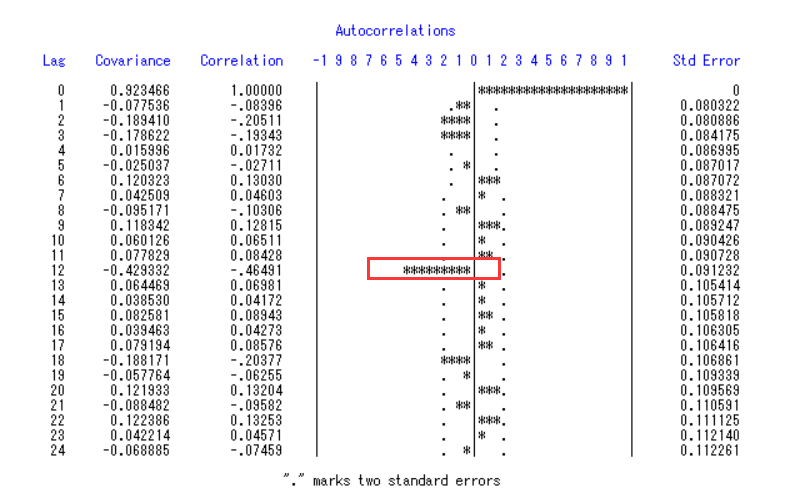
image-20200712120930111

由该自相关系数图同样可以观察到周期性减弱了许多，但仍然可能残余部分周期信息未被提取完全。我们先认为序列为平稳序列，对其进行白噪声检验。

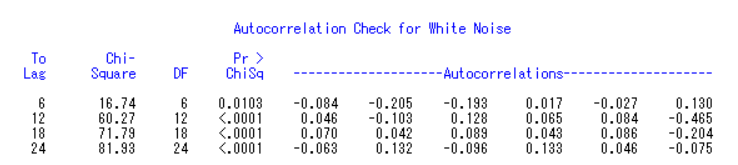
image-20200712121156624

4、因为数据序列为平稳序列且为非白噪声序列，所以数据间存在一定的相关性，我们决定先尝试使用ARIMA 模型中的简单季节模型进行预测

1
identify var=x(1,12) minic p=(0:5) q=(0:5);

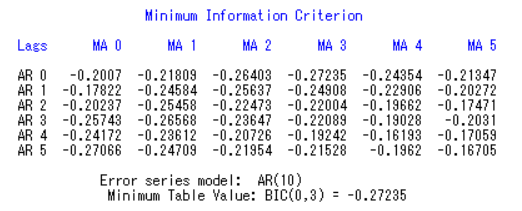
image-20200712121504800

由上表可知，当p=0,q=3 时，模型最优。模型为ARMA(0,3)。

5、接下来进行参数估计：

1
estimate p=0 q=3;

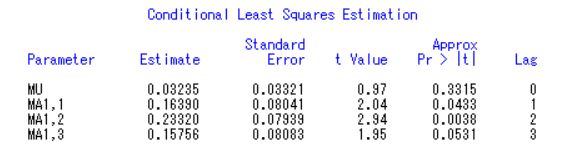
image-20200712121800765

由上参数检验表可知常数 、q=3 的P 值＞0.05，参数不通过检验。因此删除上述未通过检验的参数再进行检验

1
estimate p=0 q=2 noint;

image-20200712121952807

参数全部通过检验，接着对模型进行显著性检验，即对残差进行白噪声检验

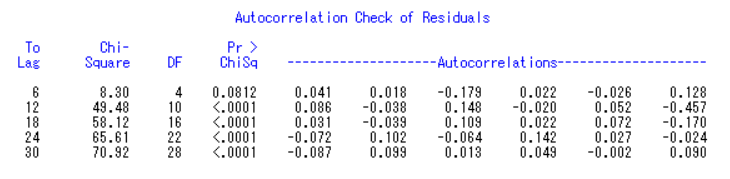
image-20200712122048269

很多都小于0.05，说明残差之间有信息传递。此模型并不适用，因此，我们选择使用ARIMA 模型中的乘积季节模型进行预测。

6、这里我们使得P、Q=0……5来一个个看，发现D(步数)等于12时均不能达到，我们这时候可以把D=2，即看成24步，再次来算就容易多了

最终确定为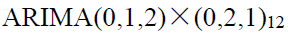image-20200712141948656

参数检验表：

image-20200712142006529

残差序列检验表：

image-20200712142025155

image-20200712142051379

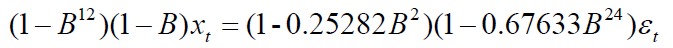
该模型的方程为：image-20200712142112187

7、得到模型我们就可以做预测了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
goptions vsize=7cm hsize=10cm;
data a;
input x@@;
dif1_12=dif12(dif(x));
time=_n_;
cards;
数据区
;
proc gplot;
plot x*time dif1_12*time;
symbol c=black i=join v=star;
proc arima;
identify var=x(1,24) minic p=(0:5) q=(0:5);
estimate p=(0) q=(2)(24) noint;
forecast lead=12 id=time out=out;
proc gplot data=out;
plot x*time=1 forecast*time=2 /overlay;
symbol1 c=black i=none v=star;
symbol2 c=red i=join v=none;
run;

预测结果如下表所示：

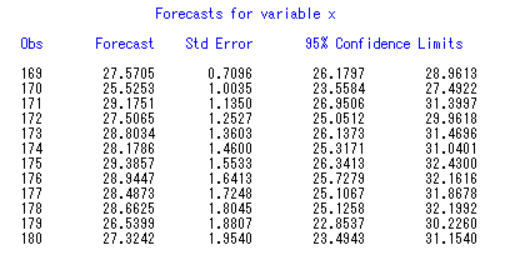
image-20200712142543568

通过预测数据绘制除原数据与预测数据的拟合曲线如下图：

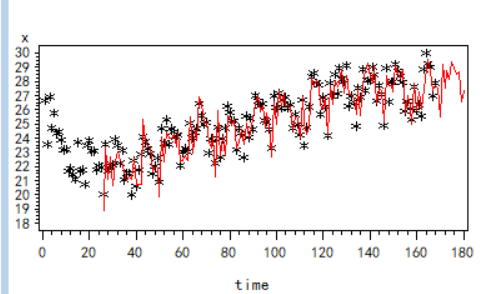
image-20200712142612981

由预测曲线图可以看出，大部分原数据在预测曲线上，预测趋势与原数据走势基本相似。
不在预测曲线上的数据几乎全部落在95%的预测曲线内，预测效果较好。

结语

鉴于本人最近嘴唇有了溃疡，决定鸽几天数学建模，看看品优购舒服一下(‾◡◝)

赏

谢谢你请我吃糖果

支付宝
微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

很惭愧<br><br>只做了一点微小的工作<br>谢谢大家