概述
本文是我大二算法分析实验的综合大实验,可能跟大家的比起来难度微不足道,希望能对你有帮助🤪
0/1背包
问题描述:
给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为C。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
对于一种物品,要么装入背包,要么不装。所以对于一种物品的装入状态可以取0和1.我们设物品i的装入状态为xi,xi∈ (0,1),此问题称为0-1背包问题。
1.递归求解
我们用F(n,C)表示将前n个物品放进容量为C的背包里,得到的最大的价值。
我们用自顶向下的角度来看,假如我们已经进行到了最后一步(即求解将n个物品放到背包里获得的最大价值),此时我们便有两种选择
- 不放第n个物品,此时总价值为F(n-1,C)
- 放置第n个物品,此时总价值为Vn+F(n-1,C-Wn)
两种选择中总价值最大的方案就是我们的最终方案:F(i,C)=max(F(i−1,C),v(i)+F(i−1,C−w(i)))
1 | /** |
2.记忆化搜索(自顶向下备忘录法)
我们可以将已经求得的子问题的结果保存下来,这样对子问题只会求解一次
1 | /** |
3.动态规划算法
通过反证法可证明此问题符合动态规划算法的最优子结构性质,可以通过动态规划来求解。了解动态规划


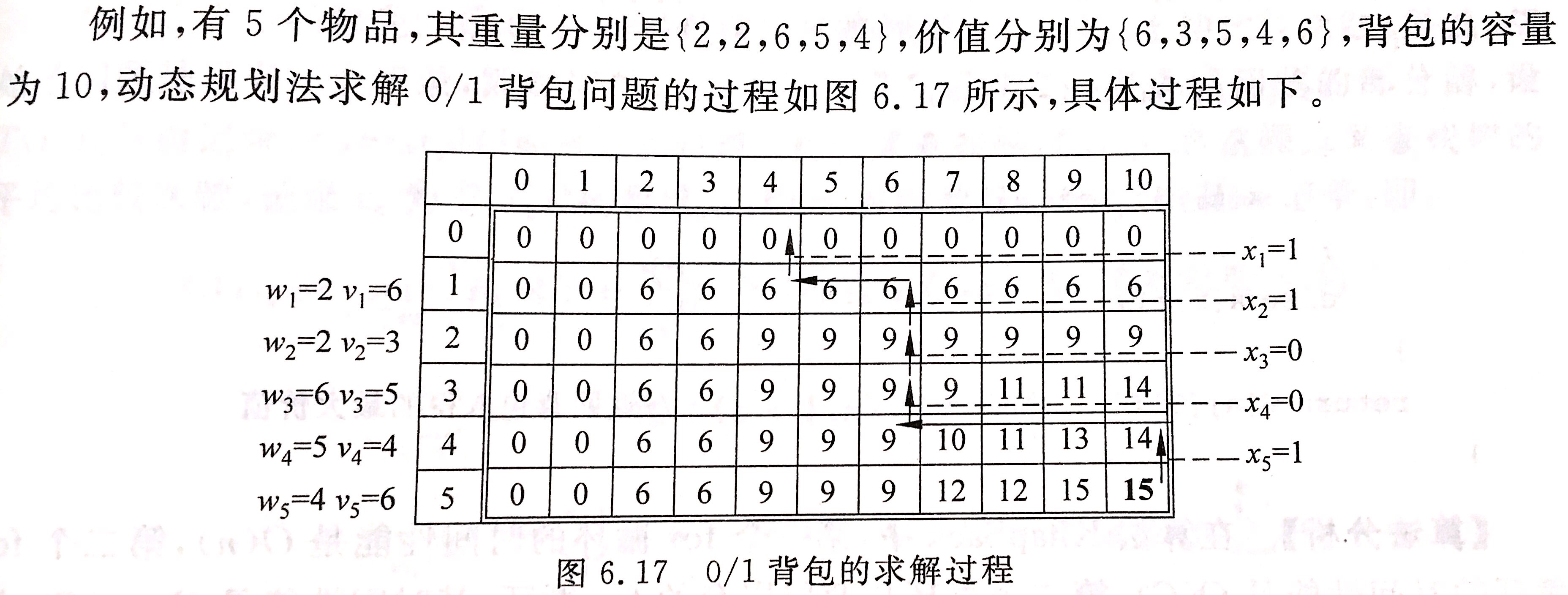
1 | /** |
4.动态规划的空间优化
上面的动态规划算法使用了O(n*C)的空间复杂度(因为我们使用了二维数组来记录子问题的解),其实我们完全可以只使用一维数组来存放结果,但同时我们需要注意的是,为了防止计算结果被覆盖,我们必须从后向前分别进行计算
我们可以知道,当我们利用一维数组进行记忆化的时候,我们只需要使用到当前位置的值和该位置之前的值,举个例子:假设我们要计算F(i,4),我们需要用到的值为F(i−1,4)和F(i−1,4−w(i)),因此为了防止结果被覆盖,我们需要从后向前依次计算结果
为保证每个物品只能使用一次,我们倒序遍历所有j的值,这样在更新dp[j]的时候,dp[j-list[i].w]的值尚未被修改,就不会出现一个物品重复使用的问题。
优化后的状态转移方程:dp[j] = max{ dp[j-list[i].w] + v, dp[j] }
1 | /** |
复杂度分析:其状态数量为nC, n为物品数量,C为背包总体积,状态转移复杂度为O(1),所以综合时间复杂度为O(n*C),优化后的空间复杂度仅为O(C)。
5.回溯法
回溯法:为了避免生成那些不可能产生最佳解的问题状态,要不断地利用限界函数(bounding function)来处死那些实际上不可能产生所需解的活结点,以减少问题的计算量。这种具有限界函数的深度优先生成法称为回溯法。
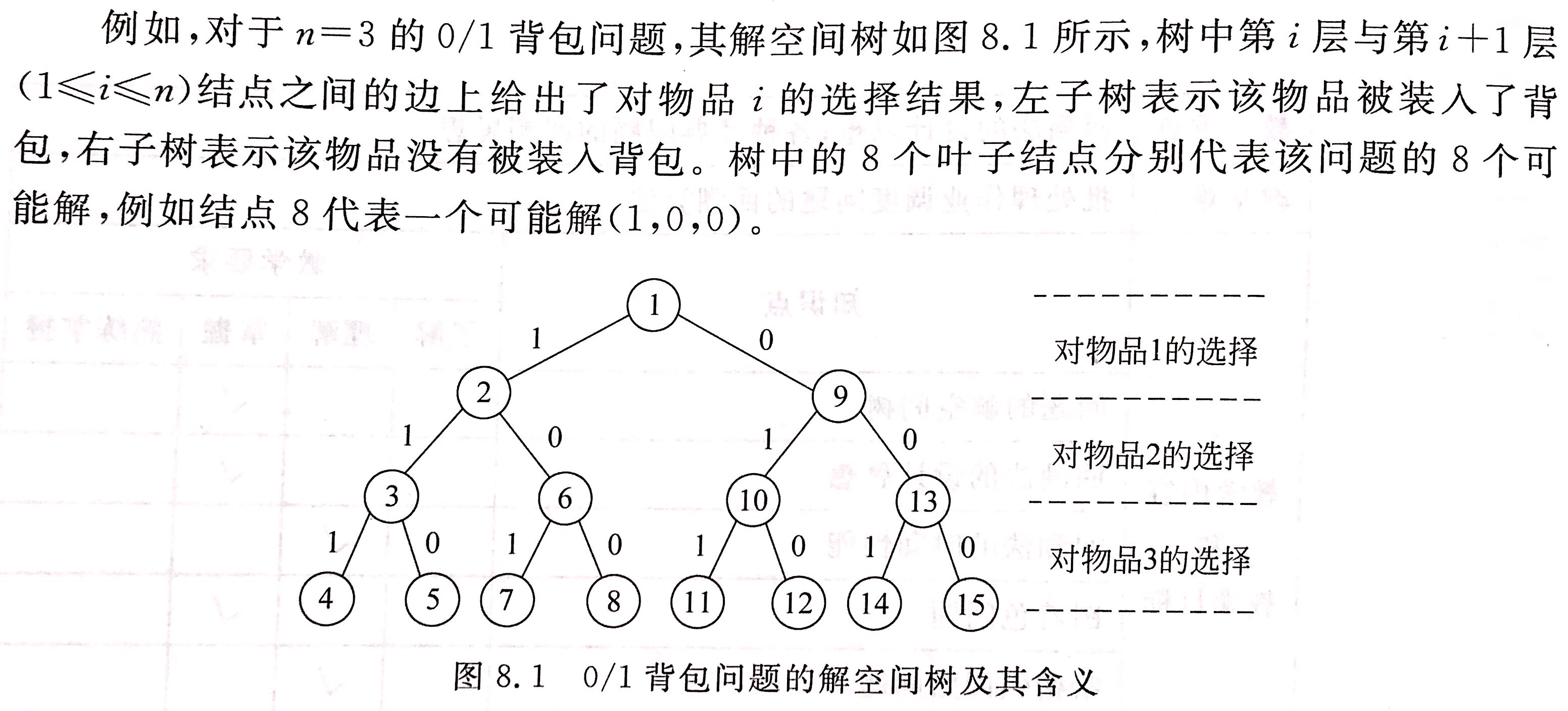
对于有n种可选物品的0/1背包问题,其解空间由长度为n的0-1向量组成,可用子集数表示。同时在构建树过程中还需考虑容量是否够来判断有无右子树。在搜索解空间树时,只要其左儿子结点是一个可行结点,搜索就进入左子树。当右子树中有可能包含最优解时就进入右子树搜索。
这里所谓回溯就是进入之后比较一下看看有没有进错,进错了就回溯回去进另一个。
这里给出思想,时间紧急,明天就要交实验报告了,代码日后研究填坑。
完全背包
问题描述:
有N种物品和一个容量为T的背包,每种物品都就可以选择任意多个,第i种物品的价值为v[i],体积为w[i],求解:选哪些物品放入背包,可卡因使得这些物品的价值最大,并且体积总和不超过背包容量。
跟01背包一样,完全背包也是一个很经典的动态规划问题,不同的地方在于01背包问题中,每件物品最多选择一件,而在完全背包问题中,只要背包装得下,每件物品可以选择任意多件。从每件物品的角度来说,与之相关的策略已经不再是选或者不选了,而是有取0件、取1件、取2件…直到取⌊T/Vi⌋(向下取整)件。
1.分析贪心算法的可行性
看到可以选择任意多件,你也许会想,那还不容易,选性价比最高的就好了。
于是开启贪婪模式,把每种物品的价格除以体积来算出它们各自的性价比,然后只选择性价比最高的物品放入背包中。
嗯,听起来好像没什么毛病,但仍旧有一个问题,那就是同一种物品虽然可以选择任意多件,但仍旧只能以件为单位,也就是说单个物品是无法拆分的,不能选择半件,只能多选一件或者少选一件。这样就造成了一个问题,往往无法用性价比最高的物品来装满整个背包,比如背包空间为10,性价比最高的物品占用空间为7,那么剩下的空间该如何填充呢?
你当然会想到用性价比第二高的物品填充,如果仍旧无法填满,那就依次用第三、第四性价比物品来填充。
听起来似乎可行,但我只需要举一个反例便能证明这个策略行不通。
想要举反例很简单,比如只有两个物品:物品A:价值5,体积5,物品B:价值8:体积7,背包容量为10,物品B的性价比显然要比物品A高,那么用贪心算法必然会选择放入一个物品B,此时,剩余的空间已无法装下A或者B,所以得到的最高价值为8,而实际上,选择放入两个物品A即可得到更高的价值10。所以这里贪心算法并不适用。
以上形象的分析摘自弗兰克的猫博主的话
2.递归法
我们只需要找到递推关系式,就很容易使用递归解法来求解了。
ks(i,t) = max{ks(i-1,t),ks(i-1, t - V[i] k) + P[i] k}; (0 <= k * V[i] <= t)
1 | /** |
如果你对比一下01背包问题中的递归解法,就会发现唯一的区别便是这里多了一层循环,因为01背包中,对于第i个物品只有选和不选两种情况,只需要从这两种选择中选出最优的即可,而完全背包问题则需要在k种选择中选出最优解,这便是最内层循环在做的事情。
3.动态规划
那这个问题可以不可以像01背包问题一样使用动态规划来求解呢?来证明一下即可。
首先,先用反证法证明最优化原理:
假设完全背包的解为F(n1,n2,…,nN)(n1,n2 分别代表第1、第2件物品的选取数量),完全背包的子问题为,将前i种物品放入容量为t的背包并取得最大价值,其对应的解为:F(n1,n2,…,ni),假设该解不是子问题的最优解,即存在另一组解F(m1,m2,…,mi),使得F(m1,m2,…,mi) > F(n1,n2,…,ni),那么F(m1,m2,…,mi,…,nN) 必然大于 F(n1,n2,…,nN),因此 F(n1,n2,…,nN) 不是原问题的最优解,与原假设不符,所以F(n1,n2,…,ni)必然是子问题的最优解。
再来看看无后效性:
对于子问题的任意解,都不会影响后续子问题的解,也就是说,前i种物品如何选择,只要最终的剩余背包空间不变,就不会影响后面物品的选择。即满足无后效性。
因此,完全背包问题也可以使用动态规划来解决。
3.1自上而下记忆法
1 | /** |
3.2自底向上填表法
1 | /** |
3.3动态规划的空间优化
跟01背包问题一样,完全背包的空间复杂度也可以进行优化,具体思路这里就不重复介绍了,可以翻看前面的01背包问题优化。
1 | /** |
其实完全背包问题也可以转化成01背包问题来求解,因为第i件物品最多选 ⌊T/Vi⌋(向下取整) 件,于是可以把第i种物品转化为⌊T/Vi⌋件体积和价值相同的物品,然后再来求解这个01背包问题。具体方法这里就不多说了,留给大家自行解决。
多重背包
问题描述:
有N种物品和一个容量为T的背包,第i种物品最多有M[i]件可用,价值为v[i],体积为w[i],求解:选哪些物品放入背包,可以使得这些物品的价值最大,并且体积总和不超过背包容量。
对比一下完全背包,其实只是多了一个限制条件,完全背包问题中,物品可以选择任意多件,只要你装得下,装多少件都行。
1.递归法
都是老菜了,直接上桌:
1 | ks(i,t) = max{ks(i-1, t - V[i] * k) + P[i] * k}; (0 <= k <= M[i] && 0 <= k * V[i] <= t) |
1 | private int ks(int i, int t){ |
2.动态规划
仅仅多了一个判断条件而已,所以只要弄懂了完全背包,多重背包就不值一提了。
2.1自上而下记忆法
1 | private int ks2(int i, int t){ |
2.2自下而上填表法
1 | public void solve3() { |
2.3优化空间
1 | private int ksp(int i, int t){ |
贪心解决0/1背包问题
问题描述:
随机生成500个0/1背包问题(问题规模可以相对较小),如果使用贪心算法进行求解,统计能够求得最优值的概率,没有求得最优值,统计最坏的情况误差有多大。实验结果跟实验设置的参数(如:背包容量)关系很大,简要分析参数对结果的影响。
1.分析
贪心算法求解背包问题的话前文也提到过,优先选择性价比最高的,选中或者不行再考虑性价比第二,第三……
用贪心算法处理这个问题的难点在于如何知道第几个性价比最高(这个很容易实现),性价比第二,第三……(有难度)
我们想到了可以将价格、重量、性价比都封装到一个对象中,这个对象在组成一个对象数组,这样通过对对象数组中性价比成员的排序,我们可以得到对应的价格重量。当然,我们还有一种更简便的方法:使用数据结构MAP,键是性价比,值是索引,来得到和之前一样的效果。(空指针异常,原因未知)
下面我们分析这个随机生成500个由哪些随机参数组成随机性:背包容量是必须的,而背包容量的确定我们可以参照物品个数及物品的重量区间,每个物品只有选择和被选择,所以我们确定背包容量时折个中,确保随机性。
我们选择4~12个物体,每个物体的重量区间为[5~20],背包容量根据物体个数*区间中位数13获得,物体的价值在1~20之间。
2.贪心算法实现
创建Knapsack对象
1 | public class Knapsack implements Comparable<Knapsack> { |
算法实现(注释为失败的尝试😭)
1 | private static int greedy(int[] w,int[] v,int C) { |
3.测试
1 | public static void main(String[] args) { |

结语
以上就是本学期最后一个实验呐,算法的路还很长,我只是刚刚踏入海滩拾贝而已,真正的深海等着我去翻越。老实说,这是我这学期最上心的一门课了(虽然也是一节课没听),希望我微薄的努力不要白费吧😁给个好分数吧老师!!!!这个对我真的很重要啊啊啊啊啊啊


